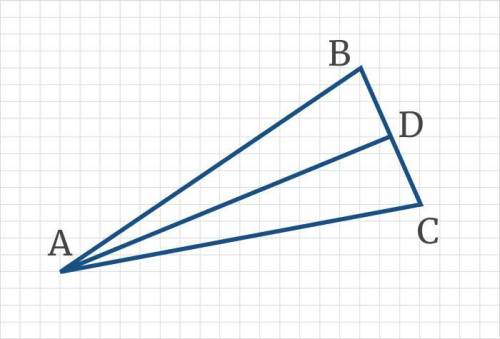
∆ABC – равнобедренный, АВ = AС, AD – медиана. Периметр ΔABC равен 60 см, а периметр ΔABD – 40 см. Какова длина медианы AD?

Добрый день! Я буду рад выступить в роли вашего школьного учителя и помочь вам разобраться с этим вопросом.

Для начала, давайте вспомним основные понятия, которые нам понадобятся для решения этой задачи.

1. Равнобедренный треугольник - это треугольник, у которого две стороны равны друг другу.
2. Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
3. Периметр треугольника - это сумма длин всех его сторон.

Теперь перейдем к решению задачи.

Дано, что треугольник ∆ABC является равнобедренным, то есть сторона AB равна стороне AC. Пусть длина стороны AB (или AC) равна x. Тогда мы можем записать периметр треугольника ∆ABC следующим образом:

AB + AC + BC = 60 см.

Учитывая, что AB = AC = x, мы можем записать это следующим образом:

2x + BC = 60

Затем у нас есть треугольник ∆ABD, в котором периметр равен 40 см. Запишем эту информацию:

AB + BD + AD = 40 см.

Учтем, что AB = x и что AD является медианой треугольника ∆ABC, которая разделяет сторону BC пополам. То есть BD = BC/2. Теперь мы можем записать данное равенство следующим образом:

x + BC/2 + AD = 40

Теперь у нас есть две уравнения с двумя неизвестными (x и BC). Мы можем решить их, чтобы найти значения этих неизвестных. Для этого преобразуем уравнения:

Сначала выразим BC через x из первого уравнения:

BC = 60 - 2x

Подставим это значение во второе уравнение:

x + (60 - 2x)/2 + AD = 40

Распределим сложение:

x + 30 - x + 2AD = 40

Упростим выражение:

30 + 2AD = 40

Вычтем 30 из обеих сторон:

2AD = 10

Разделим обе стороны на 2:

AD = 5

Таким образом, длина медианы AD равна 5 см.

Надеюсь, что я понятно объяснил решение этой задачи. Если у вас возникнут еще вопросы или что-то осталось непонятным, пожалуйста, спросите меня. Я всегда готов помочь вам в учебе.