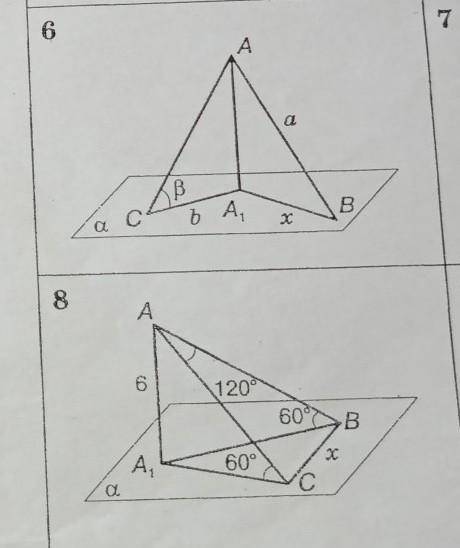
АА1 перпендикулярна до площини L, АВ і АС похилі. Знайти х і у.
Два малюнка

​

Для решения данной задачи, нам необходимо разобраться в определениях и свойствах перпендикулярных линий и плоскостей.

Перпендикулярные линии - это линии, которые пересекаются под прямым углом (или 90 градусов).

Перпендикулярные плоскости - это плоскости, которые пересекаются под прямым углом (или 90 градусов).

В данной задаче у нас есть три плоскости - плоскость АВС, плоскость АА1С1 и плоскость L. Нам необходимо найти значения х и у.

Суть данной задачи заключается в том, что плоскость АА1С1 перпендикулярна плоскости L и плоскости АВС.

Для его решения нам необходимо использовать свойство перпендикулярных плоскостей:

Если плоскость α перпендикулярна плоскости β и плоскости γ, а линия л пересекает α, β и γ, то линия л перпендикулярна обеим плоскостям β и γ.

Согласно данному свойству, мы можем сделать вывод, что линия А1С1, которая пересекает все три плоскости АА1С1, L и АВС, является перпендикулярной как плоскости L, так и плоскости АВС.

Теперь рассмотрим малюнок под номером 2. На данном малюнке мы видим, что линия А1С1 проходит через точки В, С и С1.

Нам необходимо найти значения х и у. Для этого мы можем использовать координаты точек.

Обозначим точку В как (x1, y1, z1), точку С1 как (x2, y2, z2), и точку С как (x3, y3, z3).

Согласно условиям задачи, плоскость АВС считаем произвольной, поэтому мы не знаем ее точные координаты.

Также, согласно условию, плоскость АА1С1 перпендикулярна плоскости L. Пусть координаты точек А и А1 в плоскости АА1С1 будут (0, 0, 0) и (x, y, z) соответственно.

Теперь можем записать уравнения прямых, проходящих через соответствующие точки:

Прямая, проходящая через В и С: (x - x1) / (x3 - x1) = (y - y1) / (y3 - y1) = (z - z1) / (z3 - z1)

Прямая, проходящая через В и С1: (x - x1) / (x2 - x1) = (y - y1) / (y2 - y1) = (z - z1) / (z2 - z1)

Из уравнений можно сделать вывод, что координаты точек x, y и z должны удовлетворять начальным условиям линий (прямых), а также условиям плоскостей.

Теперь нам необходимо представить уравнение плоскости L и плоскости АВС в виде общего уравнения плоскости.

Уравнение плоскости L имеет вид: Ax + By + Cz + D = 0, где A, B, C и D - это коэффициенты, определяющие уравнение плоскости.

Аналогично уравнение плоскости АВС: A'x + B'y + C'z + D' = 0.

Теперь, с учетом всех этих данных и начальных условий, мы можем составить систему уравнений и решить ее методом подстановки или методом Крамера.

Я надеюсь, что мое объяснение было понятным и достаточно подробным.