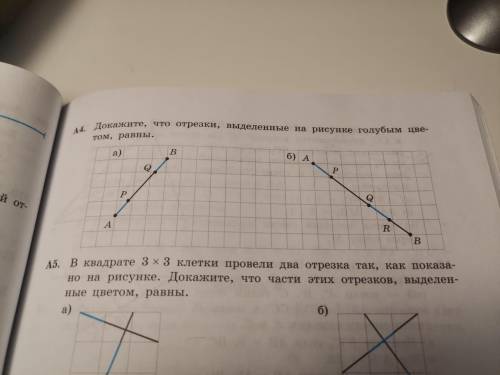
A4 (б)
Докажите, что отрезки, выделенные голубым цветом равны (использовать теорему Фаллеса)

Добрый день! Для доказательства равенства отрезков, выделенных голубым цветом, воспользуемся теоремой Фаллеса.

Теорема Фаллеса: Если два отрезка, проведенных от середин основания треугольника к точкам, расположенным на противоположных сторонах в равных участках этих сторон, то эти отрезки равны между собой.

Чтобы начать доказательство, обратим внимание на данную фигуру. Заметим, что нам нужно доказать равенство отрезков AB и AC.

Поскольку нам дано, что точка M - середина отрезка BC, то можно заметить, что AM является медианой треугольника ABC.

Так как AM - медиана, она делит BC пополам. То есть BM = MC.

Теперь рассмотрим треугольник ABC. Для доказательства равенства отрезков AB и AC, по теореме Фаллеса, нам необходимо провести отрезки, исходящие от середины основания треугольника (точка M) к точкам, расположенным на противоположных сторонах (точки B и C) в равных участках этих сторон.

Итак, рассмотрим отрезок AM. Поскольку точка M - середина отрезка BC, то отрезок AM делит BC пополам. Значит, точка M является серединой отрезка BC и разделяет его на две равные части - BM и MC. То есть BM = MC.

Так как BM = MC, а AM - общая сторона, у треугольников ABM и ACM равные стороны и общая сторона, следовательно, эти треугольники равны по двум сторонам и общей между ними.

Из равенства треугольников ABM и ACM следует, что их соответствующие стороны равны. Значит, отрезки AB и AC равны друг другу.

Таким образом, мы доказали, что отрезки AB и AC, выделенные голубым цветом, равны между собой, используя теорему Фаллеса и следующие шаги доказательства:
1. Показали, что AM - медиана треугольника ABC, поскольку точка M является серединой отрезка BC.
2. Доказали, что BM = MC, так как точка M делит отрезок BC пополам.
3. Применили теорему Фаллеса, утверждающую, что отрезки, проведенные от середин основания треугольника к точкам, расположенным на противоположных сторонах в равных участках, равны между собой.
4. Заключили, что отрезки AB и AC равны между собой, так как треугольники ABM и ACM равны по двум сторонам и общей между ними.

Надеюсь, ответ был понятен для вас. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их!