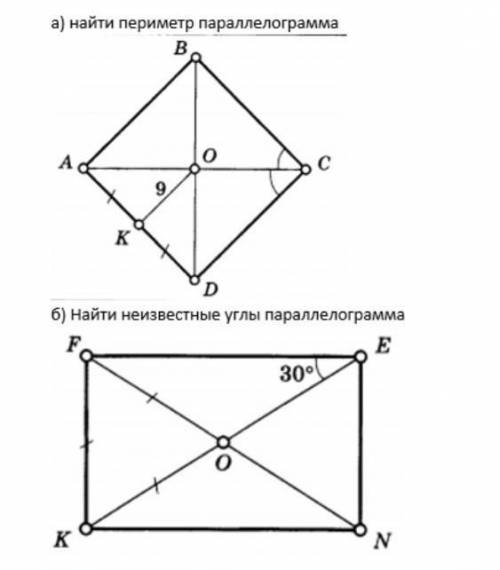
А) найдите периметр параллелограмма б) найдите неизвестные углы параллелограмма
очень надо! С РЕШЕНИЕМ!
​

Добрый день! Очень рад помочь вам с решением этой задачи.

Для начала, давайте разберемся, что такое периметр параллелограмма. Периметр - это сумма длин всех сторон фигуры. В параллелограмме у нас есть две пары параллельных сторон. Пусть одна из этих параллельных сторон имеет длину а, а вторая параллельная сторона имеет длину b.

Периметр параллелограмма, таким образом, можно найти, просто сложив длины всех четырех сторон. В нашем случае, поскольку у нас стороны a и b параллельны, мы имеем:

Периметр = a + b + a + b = 2a + 2b.

Теперь давайте найдем значения сторон a и b. Для этого обратимся к изображению, которое вы предоставили.

Мы видим, что одна из сторон параллелограмма указана как 5см. Давайте обозначим ее как a. Теперь нам нужно найти длину второй стороны b.

Изображение показывает, что у нас есть две пары вертикальных углов между сторонами a и b. Эти углы имеют одинаковую меру и обозначены как z.

Сумма углов в параллелограмме равна 360 градусов. У нас есть два параллельных угла z между сторонами a и b. Таким образом у нас есть:

2z + 2z = 360 градусов.

Поскольку сумма углов равна 360 градусов, мы можем разделить это равенство на 2:

2z = 360 градусов / 2 = 180 градусов.

Теперь, чтобы найти значение угла z, давайте разделим обе стороны на 2:

z = 180 градусов / 2 = 90 градусов.

Таким образом, у нас есть прямой угол между сторонами a и b.

Теперь, чтобы найти длину стороны b, мы можем использовать теорему Пифагора. Мы знаем, что у нас есть прямой угол между сторонами a и b, поэтому мы можем использовать теорему Пифагора, чтобы найти сторону b.

Теорема Пифагора гласит:
a^2 + b^2 = c^2.

Мы знаем, что сторона a равна 5 см (как указано на изображении). Заменим значение a в уравнении теоремы Пифагора:

5^2 + b^2 = c^2.

Решим это уравнение для b. Возведем 5 в квадрат:

25 + b^2 = c^2.

На этом этапе нам необходимо знать значение стороны, которую мы обозначаем как c, но на изображении это значение не указано. Если у вас есть это значение, то подставьте его в формулу. Если нет, давайте заменим значение c буквой, например, d:

25 + b^2 = d^2.

Теперь, чтобы найти длину стороны b, нам нужно вычесть 25 из обеих сторон уравнения:

b^2 = d^2 - 25.

Теперь возьмем квадратный корень от обеих сторон уравнения, чтобы найти значение стороны b:

b = sqrt(d^2 - 25).

Таким образом, мы нашли значение стороны b.

Теперь, когда у нас есть значения сторон a и b, мы можем найти периметр параллелограмма:

Периметр = 2a + 2b.

Подставим значения a и b в формулу:

Периметр = 2 * 5 см + 2 * sqrt(d^2 - 25) см.

Таким образом, мы нашли периметр параллелограмма.

Чтобы найти неизвестные углы параллелограмма, мы можем использовать знание о свойствах углов в параллелограмме. У параллелограмма противоположные углы равны между собой, а смежные углы сумма которых равна 180 градусов.

Поскольку мы знаем, что у нас есть прямой угол в параллелограмме (90 градусов), мы можем использовать это свойство, чтобы найти значения остальных углов.

Обозначим неизвестные углы как x и y.

Так как углы противоположные находятся напротив друг друга, мы имеем уравнения:

x = 90 градусов,
y = 90 градусов.

Теперь мы можем использовать свойство, что смежные углы сумма которых равна 180 градусов, чтобы найти остальные углы.

Мы уже знаем значение угла z - 90 градусов. Таким образом, у нас есть:

x + z = 180 градусов,
y + z = 180 градусов.

Подставим известные значения:

90 градусов + z = 180 градусов,
y + 90 градусов = 180 градусов.

Решим эти уравнения:

z = 180 градусов - 90 градусов = 90 градусов,
y = 180 градусов - 90 градусов = 90 градусов.

Таким образом, мы нашли значения углов x, y и z.

Надеюсь, эта подробная и обстоятельная информация помогла вам понять и решить задачу. Если у вас возникли еще какие-либо вопросы, буду рад помочь!