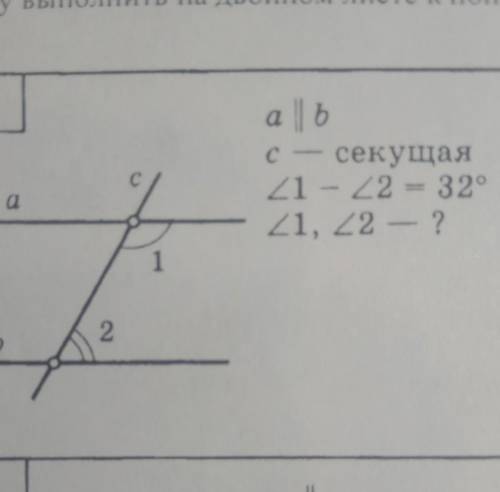
А||b
c- секущая
угол 1-угол2=32градусам
угол1,угол2-?​

∠1=96°

∠2=74°

Объяснение:

∠1+∠2=180°; ∠1=∠2+32°; ∠2+32+∠2=180°; ∠2=(180°+32)/2=74°

∠1=74*32=96°

Для решения этой задачи, нам потребуется знание о геометрических свойствах секущих и о трехугольнике. Поэтому мы рассмотрим задачу пошагово.

Шаг 1: Вспомним о свойствах секущих
В данной задаче АВ является секущей, то есть прямой, которая пересекает окружность в двух точках (точка В в нашем случае). Мы знаем, что угол, образованный секущей и хордой, равен половине суммы дуг, заключенных между секущей и этой хордой.

Шаг 2: Угол, образованный АВ и секущей
У нас даны угол 1 и угол 2, причем известно, что угол 1 - угол 2 = 32 градуса. Угол 1 и угол 2 образуют угол, который мы будем называть углом 3. Таким образом, мы можем записать уравнение:
угол 1 - угол 2 = угол 3
32 градуса = угол 3

Шаг 3: Образуем уравнение с помощью дуг
Так как угол 1 и угол 2 образуют угол 3, мы можем записать уравнение, используя дуги, которые они заключают. Дуга, пересекаемая секущей АВ, находится между углом 1 и углом 3, и такая же дуга находится между углом 3 и углом 2. Обозначим эти дуги как дуга АС и дуга СВ соответственно.

Таким образом, дуга АС + дуга СВ = дуга АВ

Шаг 4: Составляем уравнение
Обозначим угол 3, который мы ищем, как угол АСВ. Тогда можем записать уравнение:
угол АСВ + угол АСВ = 32 градуса
2 * угол АСВ = 32 градуса
угол АСВ = 16 градусов

Шаг 5: Находим угол 1 и угол 2
Угол 1 = угол АСВ + угол АС (по свойствам геометрических фигур и углов при пересечении секущей и окружности)
Угол 1 = 16 градусов + угол АС (Сейчас мы будем находить угол АС)
Угол АС = угол АСВ = 16 градусов (по свойствам геометрических фигур и углов при пересечении секущей и окружности)

Угол 1 = 16 градусов + 16 градусов
Угол 1 = 32 градуса

Угол 2 = угол АС + угол СВ (по свойствам геометрических фигур и углов при пересечении секущей и окружности)
Угол 2 = 16 градусов + 16 градусов
Угол 2 = 32 градуса

Таким образом, угол 1 и угол 2 равны 32 градусам каждый.

Надеюсь, это подробное решение поможет вам понять, как решить эту задачу. Если у вас остались вопросы, не стесняйтесь задавать их.