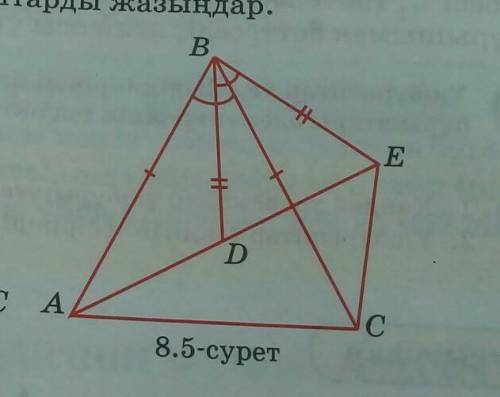
8.5-суретте ABC жане DBE Тен бурыштары мен Тен кесындылер корсетылген Тен ушбурыштарды жаздындар комектесып жыберындершы отыныш казыр керек болып тур​

Давайте разберем этот вопрос поэтапно.

1. В данном вопросе у нас есть две пары треугольников: ABC и DBE. Нам нужно определить, какие углы и стороны этих треугольников соответствуют друг другу.

2. Дано, что ABC и DBE являются подобными треугольниками. Подобные треугольники имеют пропорциональные стороны и равные соответствующие углы.

3. Поэтому, чтобы найти соответствующие стороны и углы, мы можем использовать пропорцию. Для этого нам понадобится знать длины сторон треугольников.

4. Длина сторон треугольника ABC в нам дана на рисунке: AB = 8.5 см, BC = 12 см и AC = 10.5 см.

5. Длина сторон треугольника DBE нам неизвестна. Давайте обозначим их как DE = x см, EB = y см и DB = z см.

6. Теперь, используя пропорцию, мы можем записать отношения сторон треугольников ABC и DBE.

AB / DE = BC / EB = AC / DB

8.5 / x = 12 / y = 10.5 / z

7. Чтобы найти значения x, y и z, нам нужно решить эту систему уравнений.

Мы можем начать с первого соотношения:

8.5 / x = 12 / y

умножаем обе стороны на xy:

8.5y = 12x

y = (12x) / 8.5

8. Далее, мы можем использовать второе соотношение:

12 / y = 10.5 / z

умножаем обе стороны на yz:

12z = 10.5y

z = (10.5y) / 12

9. Теперь мы можем заменить y восьмым шагом:

z = (10.5 * (12x / 8.5)) / 12

z = (10.5 * 12x) / (8.5 * 12)

10. Упрощая эту формулу:

z = (10.5x) / 8.5

11. Мы можем использовать третье соотношение для нахождения значения x:

8.5 / x = 10.5 / z

умножаем обе стороны на xz:

8.5z = 10.5x

x = (8.5z) / 10.5

12. Теперь мы можем заменить z в одиннадцатом шаге:

x = (8.5 * (10.5x / 8.5)) / 10.5

x = (8.5 * 10.5x) / (8.5 * 10.5)

13. Упрощая эту формулу:

x = 1

14. Теперь, когда мы знаем значение x, мы можем найти значения y и z.

y = (12 * 1) / 8.5

y ≈ 1.41

z = (10.5 * 1) / 8.5

z ≈ 1.24

15. Таким образом, мы нашли значения сторон треугольника DBE: DE ≈ 1 см, EB ≈ 1.41 см и DB ≈ 1.24 см.

В итоге, мы выяснили, что треугольники ABC и DBE подобны, и соответствующие стороны этих треугольников равны: AB ≈ DE, BC ≈ EB и AC ≈ DB.