5.2. некоторая прямая l перпендикулярна сторонам ab и ac треугольника abc. определите взаимное расположение прямой i и плоскости треугольнихabc: а) прямая l пересекает плоскость abc, но не перпендикулярна ей; б) прямая l принадлижит плоскости abc; в) прямая l перпендикулярнаплоскости abc; г) прямая l перпендикулярна плоскости abc.5.3. прямая ко перпендикулярна плоскости параллелограмма abcd. определите прямую, перпендикулярную прямой ко.5.4. прямая мв перпендикулярна сторонам ав и вс треугольника авс. найдите вид треугольника mbx, если точка x - произвольнаяточка стороны ас.​

5.2.  Если прямая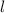    перпендикулярна двум пересекающимся прямым (АВ и АС) , лежащим в одной плоскости ( пл. треугольника АВС) , то эта прямая  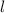  перпендикулярна самой плоскости ( пл. ΔАВС).

в) Прямая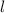    перпендикулярна плоскости треугольника АВС.

5.3.  Так как КО⊥ АВСД ( плоскости параллелограмма АВСД) , то эта прямая перпендикулярна ЛЮБОЙ прямой, лежащей в плоскости АВСД. Значит, КО⊥АВ , КО⊥ВС , КО⊥АД , КО⊥СД , КО⊥АС , КО⊥ВД ,...

5.4.  МВ⊥пл ΔАВС  ⇒  МВ перпендикулярна ЛЮБОЙ прямой, лежащей в этой плоскости АВС, в том числе МВ⊥ВХ ( Х∈АС⊂ΔАВС ) ⇒

∠МВХ=90°  и  ΔМВХ - прямоугольный .

Cм. рисунки.

5.2. Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна самой плоскости.

l⊥(ABC)

5.3. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости.

KO⊥AB, KO⊥BC, KO⊥CD, KO⊥AD

5.4. MB⊥(ABC) => MB⊥BX, ∠MBX=90