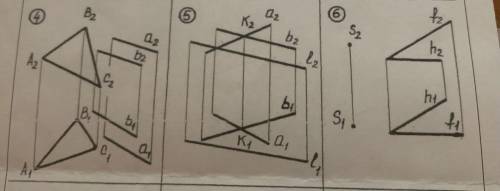
4) Построить линию пересечения двух плоскостей 5) Построить точку пересечения прямой l с плоскостью и показать её видимость

6) Определить расстояние от точки S до плоскости "A(60;110;20) B(100;25;130) C(160;40;40)"- координаты треугольника. Точка D(150;130;110)

Добрый день!

Для начала разберем каждый вопрос по отдельности.

4) Построить линию пересечения двух плоскостей.

Для построения линии пересечения двух плоскостей нужно знать уравнения этих плоскостей. Уравнение плоскости в трехмерном пространстве имеет общий вид: Ax + By + Cz + D = 0, где A, B, C - коэффициенты плоскости, а D - свободный коэффициент.

Например, пусть эти уравнения имеют вид:
Плоскость 1: 2x - 3y + z - 6 = 0
Плоскость 2: x + 4y + 2z + 8 = 0

Теперь нужно решить систему уравнений, составленную из этих плоскостей, чтобы найти линию их пересечения. Сначала систему уравнений перепишем в стандартном виде:

Плоскость 1: 2x - 3y + z = 6
Плоскость 2: x + 4y + 2z = -8

Перепишем систему в расширенную матрицу, чтобы применить метод Гаусса для решения системы:

| 2 -3 1 | |x| | 6|
| 1 4 2 | * |y| = |-8|

Сделаем преобразования строк матрицы, чтобы привести ее к ступенчатому виду:

| 1 4 2 | |y| |-8|
| 0 5 -3 | * |x| = |26|

После преобразований, получаем:
x = 4
y = -2

Теперь можем подставить значения x и y в любое из уравнений плоскостей и рассчитать значение z. Для примера, возьмем плоскость 1:
2x - 3y + z = 6
2(4) - 3(-2) + z = 6
8 + 6 + z = 6
14 + z = 6
z = 6 - 14
z = -8

Таким образом, линия пересечения двух плоскостей имеет координаты (4, -2, -8).

5) Построение точки пересечения прямой l с плоскостью и показ ее видимости.

Для построения точки пересечения прямой с плоскостью также нужно знать уравнения прямой и плоскости. Пусть у нас есть прямая l с уравнением: x = 2t, y = 3t, z = -t, где t - параметр.

И пусть у нас есть плоскость с уравнением: 2x + 3y - z = 8.

Теперь можно решить систему уравнений, составленную из прямой и плоскости:
2(2t) + 3(3t) - (-t) = 8

Раскрываем скобки и сокращаем:
4t + 9t + t = 8
14t = 8
t = 8/14
t = 4/7

Теперь можем подставить полученное значение t обратно в уравнение прямой для определения координат точки пересечения:
x = 2(4/7) = 8/7
y = 3(4/7) = 12/7
z = -(4/7) = -4/7

Таким образом, точка пересечения прямой l с плоскостью имеет координаты (8/7, 12/7, -4/7). Чтобы показать ее видимость, нужно построить график прямой на плоскости и проверить, находится ли точка на видимой стороне относительно плоскости.

6) Определить расстояние от точки S до плоскости.

Для определения расстояния от точки до плоскости, можно использовать формулу:

d = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2),

где A, B, C - коэффициенты плоскости, D - свободный коэффициент, а x, y, z - координаты точки.

Для данного примера плоскость задана уравнением 2x + 3y + z - 8 = 0. Имеются координаты точки S (60, 110, 20).

Подставим значения в формулу и рассчитаем расстояние:

d = |2(60) + 3(110) + 20 - 8| / √(2^2 + 3^2 + 1^2)
= |120 + 330 + 20 - 8| / √(4 + 9 + 1)
= |462| / √14
= 462 / √14

Таким образом, расстояние от точки S до плоскости составляет 462 / √14 единиц расстояния.

Надеюсь, я смог достаточно подробно объяснить ответы на ваши вопросы. Если у вас еще остались какие-либо вопросы, с удовольствием на них отвечу!