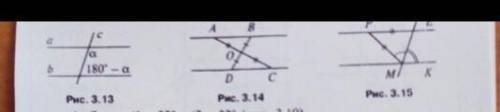
4. Доказать: a || б(рис. 3.13). 5. Доказать: АВ |CD (рис. 3.14). 6. Доказать: PE || MK (рис. 3.15).

Для решения данных задач, нам необходимо разобраться с определениями и свойствами параллельных и пересекающихся прямых.

Для начала, рассмотрим определение параллельных прямых. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются ни в одной точке. При этом, их направляющие векторы равны или пропорциональны.

Теперь рассмотрим определение пересекающихся прямых. Две прямые называются пересекающимися, если они лежат в одной плоскости и имеют общую точку пересечения.

Теперь переходим к решению данного вопроса.

4. Необходимо доказать, что прямые a и б параллельны. Для этого, мы должны убедиться, что их направляющие векторы равны или пропорциональны. Направляющие векторы можно найти, проведя прямые, указанные на рисунке (a и б), и находя вектора соединяющие две пары точек на каждой из этих прямых. Если направляющие векторы пропорциональны, то прямые параллельны.

5. Необходимо доказать, что линии АВ и СD пересекаются. Для этого, мы должны убедиться, что они имеют общую точку пересечения. Найдя уравнения данных линий, мы можем найти точку их пересечения и убедиться, что она действительно существует.

6. Необходимо доказать, что отрезки PE и MK параллельны. Для этого, мы должны убедиться, что их направляющие векторы равны или пропорциональны. Направляющие векторы можно найти, проведя отрезки PE и MK и находя вектора соединяющие две пары точек на каждом из этих отрезков. Если направляющие векторы пропорциональны, то отрезки параллельны.

Описанные выше шаги помогут решить данные вопросы и доказать, что прямые или отрезки параллельны или пересекаются.