36 см. Сумма катета и гипотенузы равна
Отношение этого катета к гипотенузе
1:2. Найдите меньший из отрезков, на
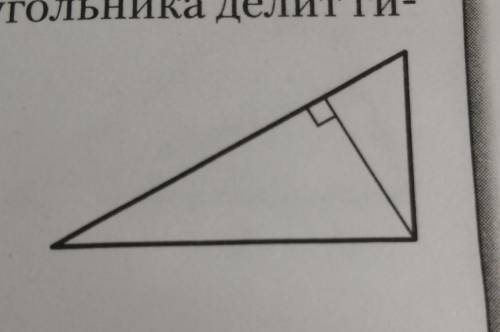
Которые высота треугольника делит ги-
потенузу.
Другие вопросы по теме Геометрия
Популярные вопросы
- нашите полное решение! 144÷×-7,6=82,4...
2 - , русский 5 класс. Простой вопрос,...
3 - Килькисть кныжок на одний полыци у 2 рази менша ниж на другий полыци якщо з 1 полыци...
3 - Как воспитывали детей римляне?...
3 - Country/ Nationality/Language знайти відповідність назвою країни та національністю...
1 - З’ясувати, скільки потрібно лимонів, щоб запрацювала світодіодна лампа потужністю...
2 - Какие непродовольственные товары недопустимы для солнечного света?...
1 - До суми чисел 1,02 і −1 1/50 додай число, обернене числу 1 1/8. Склади вираз і знайди...
3 - Твір-есе Значення досконалого володіння мовою для успішного життя( за твором Б.Шоу...
1 - Обязательно СВОИМИ СЛОВАМИ . Ни мир, ни вы сами не знаете, что именно вы совершить,...
3
6 см
Объяснение:
Задача проста і елементарна , тому її легко вирішити усно. Але покажу кілька рішень:
1)Маємо трикутник АВС , де ∠А прямий , АВ+ВС=36 см за умовою, а також АВ/ВС=1/2 якщо маємо відношення катета до гіпотенузи 1/2 , то це значить , що кут , протилежний цьому катету(∠С) =30° Це аксіома і доводити не будемо, тоді ∠В=60°
складемо рівняння: АВ+ВС=36 АВ=36-ВС 36-ВС/ВС=1/2 тоді 72=3ВС , ВС=24 (см) маємо , що гіпотенуза =24 см , тоді катет АВ=36-24=12 см
з вершини А провели висоту , і вона розділила ВС на відрізкиВМ і МС, позначимо ВМ через Х і з трикутника АВМ знайдемо ВМ ВМ=АВ* cos60°=12*1/2=6 см 6 см∠24 см , тому відрізок ВМ-найменший з відрізків і він =6 см, і відповідь така: найменший відрізок =6 см
6см
Объяснение:
Пусть дан прямоугольный треугольник АВС, где угол В -прямой.
Пусть ВК высота треугольника.
Тогда нужно найти либо АК либо КС ( мы пока не знаем, который из отрезков меньше).
Поскольку АВ/AC=cosA=1/2
то угол А =60°, значит угол С=30°.
Значит АВ<BC ( большая сторона в треугольнике лежит напротив большего угла).
Значит и проекция АВ на АС будет - это отрезок АК будет меньше, чем проекция ВС на АС ,- это отрезок КС
То есть по условию задачи нам нужно найти АК.
Итак нам известно, что АВ:АС=1:2 => AC=2*AB
AB+AC=36 => AB+2*AB=36
=>AB=12 cm
Теперь рассмотрим прямоугольный треугольник АКВ ( угол К прямой, угол А =60°)
АК=АВ*cosA
AK=12*1/2=6 см