3 задание
СМОТРЕТЬ ЗАКРЕП <3
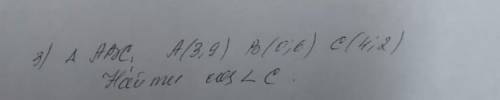
Другие вопросы по теме Геометрия
Популярные вопросы
- Возвращаясь домой из кино, вы решили сократить дорогу и пойти к...
3 - Какие опасные ситуации могут возникнуть в подъезде дома? Какие...
2 - Как вы будете действовать, если в подъезде увидели подозрительного...
3 - Какими можно определить стороны горизонта по местным признакам?...
3 - Какие правила безопасного поведения необходимо соблюдать во время...
3 - В чем заключаются особенности безопасного поведения при пользовании...
2 - В чем заключается криминогенная опасность общественного транспорта?...
3 - Какими можно добывать воду в условиях природной среды? Назовите...
2 - Как вы будете действовать, оказавшись в толпе?...
3 - Какие меры безопасности вы примите, возвращаясь поздно вечером...
3
cos∠C=→CA*→CB/(I→CAI*I→CBI) (1)
1. →CA(3-4;9-2) от координат конца вектора отняли координаты начала.
→CA(-1;7), аналогично найдем координаты →CB(0-4;6-2), получим
→CB(-4;4)
2. Найдем скалярное произведение векторов →CA*→CB=-1*(-4)+7*4=
4+28=32. перемножил соответствующие координаты и результаты сложил.
3. Найдем длины векторов →CA и →CB, возведем в квадрат координаты, сложим и извлечем корень квадратный из суммы.
I→CAI=√((-1)²+7²)√(1+49)=√50=5√2
I→CВI=√((-4)²+4²)√(16+16)=√32=4√2
4. найдем искомое значение, подставив в формулу (1) все найденные значения.
cos∠C=→CA*→CB/(I→CAI*I→CBI) =32/(5√2*4√2)=8/(5*2)=0.8
ответ 0.8