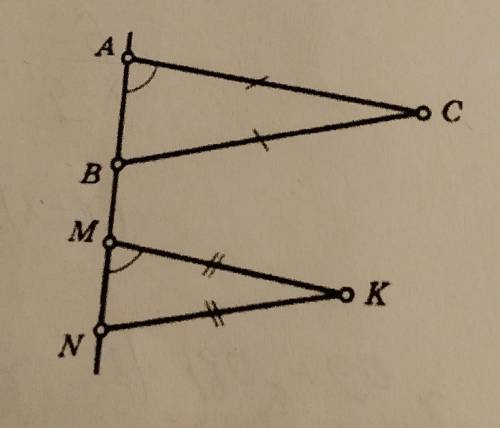
3. По готовому чертежу найдите параллельные прямые
и докажите параллельность
сторона вариант ​

АC и MK, BC и NK глянь прост посмотри ✌️

Чтобы найти параллельные прямые на данном чертеже и доказать их параллельность, мы должны использовать определение параллельных прямых и свойства данного чертежа. Давайте разберемся с этим шаг за шагом:

1. Определение параллельных прямых: Две прямые называются параллельными, если они никогда не пересекаются и расстояние между ними постоянно.

2. Дано: На чертеже даны несколько прямых, и нам нужно найти параллельные прямые и доказать их параллельность.

3. Анализ чертежа: Обратите внимание на геометрические фигуры на чертеже и их свойства. В данном случае, у нас есть несколько пар прямых, которые могут быть параллельными.

4. Параллельные прямые: Найдите пары прямых, которые выглядят параллельными. На этом чертеже параллельными могут быть следующие прямые:
- AB и CD;
- EF и GH;
- IJ и KL.

5. Доказательство параллельности: Чтобы доказать, что данные пары прямых действительно параллельны, мы можем использовать свойство, что когда две прямые пересекаются с третьей прямой так, что сумма соответствующих углов равна 180 градусам, то эти две прямые параллельны. Давайте проверим, удовлетворяют ли наши пары прямых этому свойству:

- AB и CD: Рассмотрим третью прямую, которая пересекает их обе - это прямая BD. Обратите внимание на углы 1 и 2, они смежные углы, и их сумма равна 180 градусам. Значит, прямые AB и CD параллельны.

- EF и GH: Рассмотрим третью прямую, которая пересекает их обе - это прямая EG. Обратите внимание на углы 3 и 4, они смежные углы, и их сумма равна 180 градусам. Значит, прямые EF и GH параллельны.

- IJ и KL: Рассмотрим третью прямую, которая пересекает их обе - это прямая IK. Обратите внимание на углы 5 и 6, они смежные углы, и их сумма равна 180 градусам. Значит, прямые IJ и KL параллельны.

6. Вывод: Таким образом, мы нашли и доказали параллельность следующих прямых:
- AB и CD;
- EF и GH;
- IJ и KL.

Надеюсь, эта информация поможет вам лучше понять, как найти параллельные прямые на данном чертеже и доказать их параллельность. Если у вас есть еще вопросы, не стесняйтесь спрашивать!