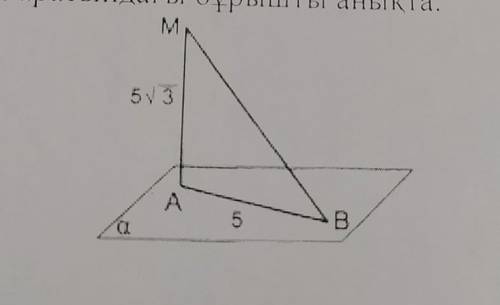
3. MB түрі а жазыктыгына перпендикуляр. Егер мВ перпендикуляры 53. келбеудин узындыгы 5 болса. МВ мен а жазыктыгы арасындагы бурышты аныкта помгите

Для решения этой задачи, нам нужно использовать знания о геометрических фигурах и свойствах перпендикуляров.

1. Из условия задачи мы знаем, что MB является перпендикуляром к ажазыктому углу. Это означает, что угол MB является прямым (90 градусов).

2. Мы также знаем, что MB и а - это стороны треугольника, а мВ - это угол противоположный стороне MB. Величина угла мВ указана в условии задачи и составляет 53 градуса.

3. Теперь мы можем использовать свойство треугольников: сумма всех углов треугольника равна 180 градусов. Так как угол мВ равен 53 градусам, то мы можем вычислить величину угла а следующим образом:

а + 90 + 53 = 180

а + 143 = 180

а = 180 - 143

а = 37 градусов

Таким образом, величина угла а равна 37 градусов.

4. Осталось найти величину боковой стороны МВ. Для этого нам нужно использовать теорему синусов, которая гласит, что отношение длины стороны к синусу противолежащего ей угла является постоянным для всех сторон треугольника.

В нашем случае, отношение длины стороны МВ к синусу угла а будет выглядеть так:

МВ / sin а = Ма / sin мВ

Подставляем известные значения:

МВ / sin 37 = 5 / sin 53

Переносим МВ налево:

МВ = 5 * (sin 37 / sin 53)

Вычисляем значение синусов:

sin 37 = 0.6018
sin 53 = 0.7992

Подставляем:

МВ = 5 * (0.6018 / 0.7992)

МВ = 3.761

Итак, длина боковой стороны МВ равна примерно 3.761

Таким образом, величина угла а равна 37 градусов, а длина боковой стороны МВ составляет около 3.761 единицы длины.