1. Геометрия
  2. 3. длина окружности равна

3. длина окружности равна . найти площадь сектора с центральным углом 40. 4. круг радиуса r=6 делится концентрической окружностью на две части - круг радиуса r и кольцо, площади которых соотносятся как 1: 3. найти r.

Oor1 Oor1    1   22.05.2019 12:00    3

Ответы
max698 max698  17.06.2020 21:39

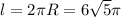
3) l=2\pi R=6\sqrt{5}\pi

R=3\sqrt{5}

S=\frac{\pi R^2}{360}\cdot40=\frac{\pi (3\sqrt{5})^2}{9}=5\pi

ответ: 5п

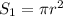
4) S_1=\pi r^2

S_2=\pi (R^2-r^2)

3S_1=S_2

3\pi r^2=\pi (R^2-r^2)

3r^2=R^2-r^2

4r^2=R^2

2r=R

r=\frac{R}{2}=\frac{6}{2} =3

ответ: 3

ПОКАЗАТЬ ОТВЕТЫ
vladpaskevits vladpaskevits  17.06.2020 21:39

Первая задача решается без вариантов, повторять ее решение нет необходимости. 


У второй задачи возможны два варианта решения.
Первый - когда площадь внутреннего круга относится к площади кольца как 1:3
Найдем площадь исходного круга:
S=πr²=36π
Тогда 3/4 этой площади занимает кольцо, 1/4- внутренний круг.
36π:4=9π- площадь внутреннего круга
S=πr²=9π
r²=9
r =3
-----------------------
Второй вариант - площадь кольца относится к площади внутреннего круга как 1:3
Тогда площадь кольца 9π,
а площадь внутреннего круга
9π*3=27π
S=πr²=27π
r²=27
r=3√3


3. длина окружности равна . найти площадь сектора с центральным углом 40. 4. круг радиуса r=6 делитс
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
kmay11 kmay11  08.03.2019 02:30
Найдите площадь фигуры, ограниченной другой окружностью и стягивающей хордой, если её дляна 6м, а дуга равна 120 градусов....
olyaperminova olyaperminova  08.03.2019 02:30
Докажите, что прямая параллельна стороне равностороннего треугольника и пересекающая две его стороны, отсекает равносторонний треугольник заранее огромное )...
chelbaeva77 chelbaeva77  08.03.2019 02:30
Точка пересечения диагоналей четырехугольника abcd является его центром симметрии. докажите, что abcd параллелограмм нужно! !...
gaytad1 gaytad1  08.03.2019 02:30
Высота конуса равна 6 см. плоскость,параллельная основанию конуса,делит образующую конуса в отношении 1: 3,считая от вершины. если площадь сечения конуса данной плоскостью равна...
magic0000 magic0000  08.03.2019 02:30
Длина окружности описанной около правельного треугольника равна 16 пи сантиметров.найдите площадь круга вписанного треугольника....
negatiff95 negatiff95  08.03.2019 02:30
Решите графически уравнение х^2=-х+6...
Эмиль08072013 Эмиль08072013  08.03.2019 02:30
Урівнобедренному трикутнику авс з основою ас кут при основі на 21 градус менший від кута при вершині.знайдіть усі кути цього трикутника....
krasatulea83 krasatulea83  08.03.2019 02:30
Надо запишите решение : стороны параллелограмма равны 4 см.,угол между ними 45 градусов. найдите высоты параллелограмма надо...
Artem0405 Artem0405  08.03.2019 02:40
Втреугольнике авс угол с = 50 градусов,угол а=20 градусо,ас = 15.решите треугольник авс и найдите его площадь....
105184 105184  19.09.2019 15:30
Дан треугольник abc с прямым углом b. найдите длину медианы bm если a) ac=10 см . б) am=8см...

Популярные вопросы