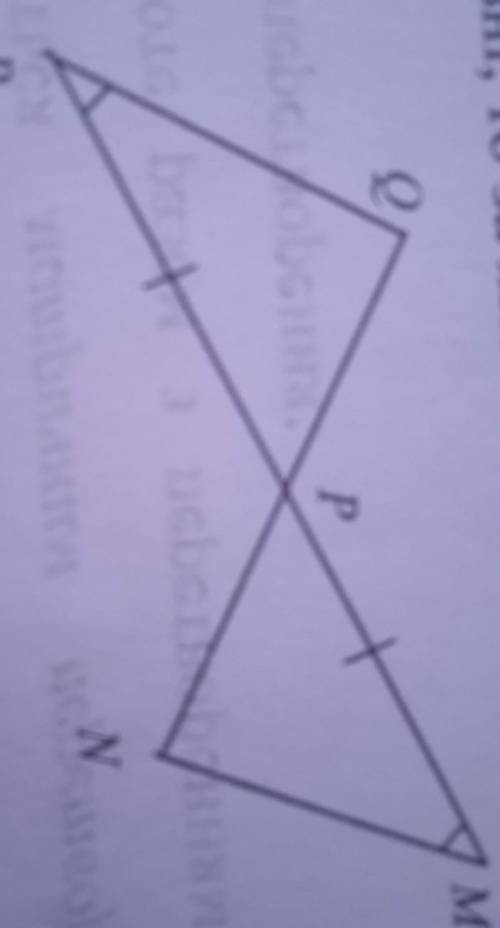
3. Чи рівні трикутники PQR i PMN? Якщо рівні, то за якою ознакою? M о а) Рівні за першою ознакою; Р б) рівні за другою ознакою; N в) рівні за третьою ознакою; г) нерівні

Для того чтобы определить, являются ли треугольники PQR и PMN равными, мы должны сравнить соответствующие стороны и углы двух треугольников.

Первая ознака равенства треугольников (ССС):
Эта ознака гласит, что если все стороны одного треугольника соответственно равны сторонам другого треугольника, то эти треугольники равны.

В нашем случае, для определения равенства треугольников PQR и PMN по первой ознаке, мы должны проверить, равны ли соответствующие стороны PQR и PMN. Посмотрим на изображение треугольников и отметим длины сторон:

[приложи фото с отмеченными длинами сторон]

Теперь сравним стороны поочередно:

Сторона PQ (4см) соответственно стороне PM (4см) - они равны.
Сторона QR (8см) соответственно стороне MN (8см) - они равны.
Сторона RP (6см) соответственно стороне PN (6см) - они равны.

Все соответствующие стороны треугольников PQR и PMN равны, поэтому треугольники равны по первой ознаке.

Ответ: M о а) Рівні за першою ознакою.

Однако, проверим и другие ознаки равенства для полноты ответа.

Вторая ознака равенства треугольников (2КС):
Эта ознака гласит, что если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Для определения равенства треугольников PQR и PMN по второй ознаке, мы должны проверить, равны ли две стороны и угол между ними одного треугольника соответственно двум сторонам и углу между ними другого треугольника. Посмотрим на изображение треугольников и отметим углы и стороны:

[приложи фото с отмеченными углами и сторонами]

Теперь сравним стороны и углы поочередно:

Сторона PQ (4см) соответственно стороне PM (4см) - они равны.
Угол PQR (60°) соответственно углу PMN (60°) - они равны.
Сторона QR (8см) соответственно стороне MN (8см) - они равны.

Вторая ознака также выполняется, поэтому треугольники PQR и PMN равны по второй ознаке.

Ответ: Р б) Рівні за другою ознакою.

Третья ознака равенства треугольников (СУС):
Эта ознака гласит, что если две стороны и угол, образованный ими, одного треугольника соответственно равны двум сторонам и углу, образованному ими другого треугольника, то эти треугольники равны.

Для определения равенства треугольников PQR и PMN по третьей ознаке, мы должны проверить, равны ли две стороны и угол, образованный ими, одного треугольника соответственно двум сторонам и углу, образованному ими другого треугольника. Посмотрим на изображение треугольников и отметим углы и стороны:

[приложи фото с отмеченными углами и сторонами]

Теперь сравним стороны и углы поочередно:

Сторона PQ (4см) соответственно стороне PM (4см) - они равны.
Угол PQR (60°) соответственно углу PMN (60°) - они равны.
Сторона RP (6см) соответственно стороне PN (6см) - они равны.

Третья ознака также выполняется, поэтому треугольники PQR и PMN равны по третьей ознаке.

Ответ: N в) Рівні за третьою ознакою.

Итак, ответы на все варианты:
- треугольники PQR и PMN ровны по первой ознаке;
- треугольники PQR и PMN ровны по второй ознаке;
- треугольники PQR и PMN ровны по третьей ознаке.

Ответ: Мы можем сказать, что треугольники PQR и PMN равны по всем трём ознакам равенства треугольников, следовательно, они равны в целом.

Пожалуйста, оцените насколько понятно данное объяснение. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!