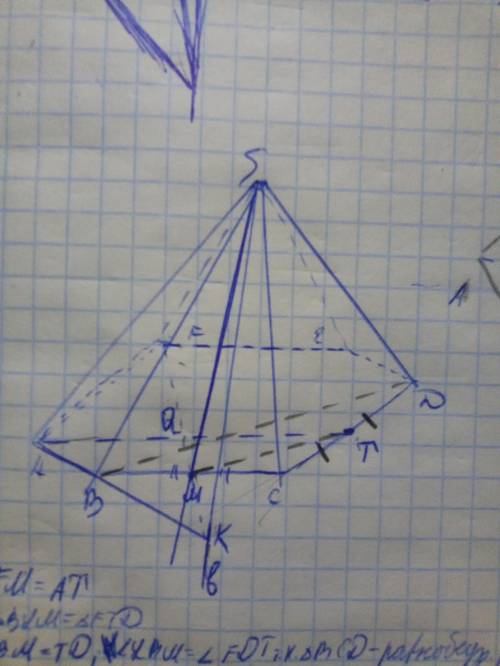
24В. Основание шестиугольной пирамиды SABCDEF — правильный
шестиугольник ABCDEF. Точка M — середина ребра BC.
а) Постройте прямую пересечения плоскостей FSM и ASB.
б) В каком отношении плоскость FSM делит отрезок, соединяющий точку A
с серединой ребра SD?

а) Чтобы построить прямую пересечения плоскостей FSM и ASB, нам необходимо найти точку пересечения этих плоскостей. Для этого обратимся к определению шестиугольной пирамиды.

Шестиугольная пирамида - это пирамида, у которой основание - шестиугольник, а ребра, исходящие из вершин основания, сходятся в одной точке - вершине пирамиды.

Также, учитывая, что точка M - середина ребра BC, мы можем сделать вывод о том, что BM = MC.

Так как основание пирамиды SABCDEF - правильный шестиугольник, то уголы основания равны между собой, и плоскости пирамиды будут симметричны относительно прямой з, проходящей через середины ребер BC и EF.

Используя эти свойства, мы можем сделать предположение о том, что плоскости FSM и ASB имеют общую прямую. Для доказательства данного предположения докажем, что прямая y, проходящая через точку M и перпендикулярная плоскости FSM, также будет перпендикулярна плоскости ASB.

Для начала, обратимся к понятию перпендикулярности плоскостей. Плоскости перпендикулярны, если прямая, пересекающая одну из них, перпендикулярна к другой плоскости. В нашем случае, прямая y перпендикулярна к плоскости FSM.

Теперь рассмотрим плоскость ASB. Для доказательства перпендикулярности прямой y и плоскости ASB, достаточно показать, что эта прямая перпендикулярна всем прямым, лежащим в данной плоскости ASB.

Сейчас мы знаем, что плоскость ASB перпендикулярна прямой x, проходящей через вершину S и середину ребра SD.

Теперь мы можем сделать вывод о том, что если прямая y перпендикулярна плоскости FSM и перпендикулярна прямой x, которая лежит в плоскости ASB, то она также будет перпендикулярна самой плоскости ASB. Ответом на задачу будет прямая y, проходящая через точку M и перпендикулярная плоскости ASB.

б) Чтобы найти отношение, в котором плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD, нам необходимо рассмотреть отношение длин отрезков, образованных этой плоскостью.

Обратимся к понятию геометрического места точек. Известно, что геометрическое место точек, равноудаленных от двух плоскостей, является прямой, перпендикулярной этим плоскостям. В нашем случае, геометрическое место точек, равноудаленных от плоскостей FSM и ASB, будет прямой линией, параллельной плоскостям FSM и ASB.

Мы уже знаем, что плоскость FSM и прямая x, проходящая через вершину S и середину ребра SD, перпендикулярны друг другу. Значит, прямая x будет являться геометрическим местом точек, равноудаленных от плоскостей FSM и ASB.

Таким образом, отношение, в котором плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD, будет равно отношению длин отрезков AMS и MSD. Для нахождения этого отношения, нам необходимо вычислить длины отрезков AMS и MSD.

Для начала, обратимся к свойству шестиугольной пирамиды. Заметим, что прямая, проходящая через вершину S и середину ребра SD, делит высоту пирамиды на две равные части. Значит, отрезки AMS и MSD равны между собой.

Поэтому отношение, в котором плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD, будет равно 1:1 или просто 1.

Таким образом, плоскость FSM делит отрезок, соединяющий точку A с серединой ребра SD, в отношении 1:1. Ответ на вопрос б) будет равен 1.