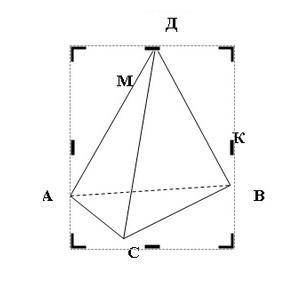
2. В тетраэдре ДАВС точка М лежит на ребре АВ, а точка К на ребре ДВ (рис. 3). Точка пересечения прямой МК и плоскости АВС лежит на прямой а) ВС; б) АВ; в) АС; г) ДС.

Для решения данной задачи, нам необходимо определить, на какой прямой лежит точка пересечения МК и плоскости АВС.

Известно, что точка М лежит на ребре АВ, а точка К на ребре ДВ.

Давайте рассмотрим возможные варианты ответов:

а) ВС - Вектор МК:
Возьмем МК: вершина К - вершина М: КМ = (КР - МР) + (КР - СК) + (РМ - СМ).
Найдем разложение КР, МР, СК и СМ на координатные векторы:
КР = (x₄ - x₂; y₄ - y₂; z₄ - z₂),
МР = (x₂ - x₅; y₂ - y₅; z₂ - z₅),
СК = (x₃ - x₄; y₃ - y₄; z₃ - z₄),
СМ = (x₃ - x₂; y₃ - y₂; z₃ - z₂).
Подставим эти значения в выражение для вектора МК:
КМ = (x₄ - x₂; y₄ - y₂; z₄ - z₂) + (x₃ - x₄; y₃ - y₄; z₃ - z₄) + (x₂ - x₅; y₂ - y₅; z₂ - z₅) + (x₃ - x₂; y₃ - y₂; z₃ - z₂),
Выполним операции поэлементного сложения:
КМ = (x₄ - x₂ + x₃ - x₄ + x₂ - x₅ + x₃ - x₂; y₄ - y₂ + y₃ - y₄ + y₂ - y₅ + y₃ - y₂; z₄ - z₂ + z₃ - z₄ + z₂ - z₅ + z₃ - z₂),
Упростим выражение:
КМ = (0; y₄ - y₅; z₃ - z₅),
Заметим, что для всех трех координат полученного вектора КМ, у нас есть только одна неизвестная - это координата у вершины С, а именно y₄.
Это означает, что точка МК будет лежать на плоскости ВС, только если координаты этой точки будут такими, что у = y₄.
Ответ: а) ВС.

б) АВ:
Поступим аналогично варианту а).
Вектор МК: вершина К - вершина М: КМ = (КР - МР) + (КР - СК) + (РМ - СМ).
Разложим векторы КР, МР, СК и СМ на координатные векторы:
КР = (x₄ - x₂; y₄ - y₂; z₄ - z₂),
МР = (x₂ - x₅; y₂ - y₅; z₂ - z₅),
СК = (x₃ - x₄; y₃ - y₄; z₃ - z₄),
СМ = (x₃ - x₂; y₃ - y₂; z₃ - z₂).
Подставляем значения и раскладываем:
КМ = (x₄ - x₂; y₄ - y₂; z₄ - z₂) + (x₃ - x₄; y₃ - y₄; z₃ - z₄) + (x₂ - x₅; y₂ - y₅; z₂ - z₅) + (x₃ - x₂; y₃ - y₂; z₃ - z₂),
Выполняем операции поэлементного сложения:
КМ = (x₄ - x₂ + x₃ - x₄ + x₂ - x₅ + x₃ - x₂; y₄ - y₂ + y₃ - y₄ + y₂ - y₅ + y₃ - y₂; z₄ - z₂ + z₃ - z₄ + z₂ - z₅ + z₃ - z₂),
Упрощаем выражение:
КМ = (0; y₃ - y₅; z₃ - z₅),
Как видно из полученного вектора КМ, все его координаты зависят только от координат вершины С, и мы видим, что значения y и z у точки М изменяются так же, как у точки С.
Это означает, что точка МК будет лежать на плоскости АВ только при условии, что значения y и z координат точки М будут такими же, как значения y и z координат вершины С.
Ответ: б) АВ.

в) АС:
Вновь воспользуемся методом разложения векторов:
Вектор МК: вершина К - вершина М: КМ = (КР - МР) + (КР - СК) + (РМ - СМ).
Разложим векторы КР, МР, СК и СМ по координатам:
КР = (x₄ - x₂; y₄ - y₂; z₄ - z₂),
МР = (x₂ - x₅; y₂ - y₅; z₂ - z₅),
СК = (x₃ - x₄; y₃ - y₄; z₃ - z₄),
СМ = (x₃ - x₂; y₃ - y₂; z₃ - z₂).
Подставим значения и раскладываем:
КМ = (x₄ - x₂; y₄ - y₂; z₄ - z₂) + (x₃ - x₄; y₃ - y₄; z₃ - z₄) + (x₂ - x₅; y₂ - y₅; z₂ - z₅) + (x₃ - x₂; y₃ - y₂; z₃ - z₂),
Выполняем операции поэлементного сложения:
КМ = (x₄ - x₂ + x₃ - x₄ + x₂ - x₅ + x₃ - x₂; y₄ - y₂ + y₃ - y₄ + y₂ - y₅ + y₃ - y₂; z₄ - z₂ + z₃ - z₄ + z₂ - z₅ + z₃ - z₂),
Упрощаем выражение:
КМ = (0; y₃ - y₅; z₄ - z₅),
Как видно из полученного вектора КМ, его первая координата всегда равна нулю, что означает, что точка МК будет находиться на плоскости АС только при условии, что x-координата точки М будет равна x-координате вершины В.
Ответ: в) АС.

г) ДС:
Проделаем аналогичные действия с разложением векторов:
Вектор МК: вершина К - вершина М: КМ = (КР - МР) + (КР - СК) + (РМ - СМ).
Векторы КР, МР, СК и СМ разложим на координатные векторы:
КР = (x₄ - x₂; y₄ - y₂; z₄ - z₂),
МР = (x₂ - x₅; y₂ - y₅; z₂ - z₅),
СК = (x₃ - x₄; y₃ - y₄; z₃ - z₄),
СМ = (x₃ - x₂; y₃ - y₂; z₃ - z₂).
Подставляем значения и рассматриваем выражение:
КМ = (x₄ - x₂; y₄ - y₂; z₄ - z₂) + (x₃ - x₄; y₃ - y₄; z₃ - z₄) + (x₂ - x₅; y₂ - y₅; z₂ - z₅) + (x₃ - x₂; y₃ - y₂; z₃ - z₂),
Выполняем операции поэлементного сложения:
КМ = (x₄ - x₂ + x₃ - x₄ + x₂ - x₅ + x₃ - x₂; y₄ - y₂ + y₃ - y₄ + y₂ - y₅ + y₃ - y₂; z₄ - z₂ + z₃ - z₄ + z₂ - z₅ + z₃ - z₂),
Упрощаем выражение:
КМ = (0; y₃ - y₅; z₃ - z₅),
Заметим, что координаты y и z точки МК совпадают с координатами y и z вершины С.
Итак, точка МК будет находиться на плоскости ДС только при условии, что значения y и z координат точки М будут такими же, как значения y и z координаты вершины С.
Ответ: г) ДС.

Таким образом, точка пересечения прямой МК и плоскости АВС будет лежать на прямой а) ВС.