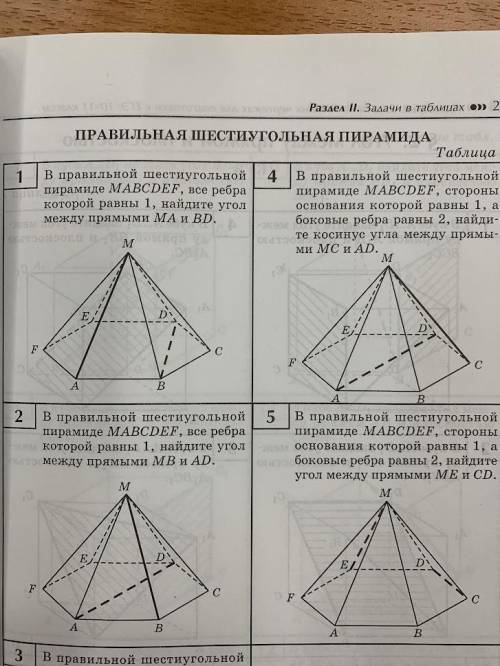
2) В правильной шестиугольной пирамиде MABCDEF, все рёбра которой равны 1, найдите угол между прямыми MA и BD

Для решения данной задачи, нам необходимо определить угол между прямыми MA и BD в правильной шестиугольной пирамиде MABCDEF, где все ребра равны 1. Давайте начнем с простого. Посмотрим на фронтальное изображение пирамиды, чтобы было понятнее какие точки соответствуют точкам A, B, C, D, E и F. Исходя из изображения, определим, что угол между прямыми MA и BD находится в плоскости, перпендикулярной плоскости этого фронтального изображения. Для того чтобы решить задачу, мы можем использовать свойство правильной шестиугольной пирамиды, которое гласит: "В правильной шестиугольной пирамиде каждый боковой грань равносторонний и равнобедренный треугольник, а длина бокового ребра (стороны треугольника) равна 1". Теперь мы можем приступить к решению. Обозначим точку O - вершину пирамиды, так как мы не знаем ее название. Плоскость, проходящая через точки M, B и D, параллельна основанию пирамиды, так как все ребра равны и она является равносторонним шестиугольником. Возьмем точку C и соединим ее с точкой O. Получим прямую OC, которая пересекает сторону CD покрывающей основание. Высота CH равна H, а искомый угол между прямыми MA и BD равен углу CHA. Давайте рассмотрим равносторонний треугольник COA: В данном равностороннем треугольнике: - Угол COA = 60 градусов (так как треугольник равносторонний) - Угол OCA = Угол OAC = 60 градусов (так как предполагаем, что C и O находятся на одинаковом расстоянии от A) - Ребро CO = Ребро AO = 1 (так как все ребра равны) Определим длину высоты H, для этого рассмотрим прямоугольный треугольник COH: В данном прямоугольном треугольнике: - Угол COH = 90 градусов (так как одна из сторон пересекает основание под прямым углом) - Угол CHA = Угол OCA = 60 градусов (по свойству равностороннего треугольника) - Ребро CO = Ребро AO = 1 (так как все ребра равны) Теперь мы можем использовать тригонометрию для нахождения длины высоты H. Воспользуемся тангенсом: tg(CHA) = H / CO Так как мы знаем, что tg(60 градусов) = √3, подставим значения в формулу: √3 = H / 1 Отсюда можем найти высоту H: H = √3 Теперь мы можем определить искомый угол между прямыми MA и BD. Рассмотрим прямоугольный треугольник CHA: В данном прямоугольном треугольнике: - Угол CHA = 60 градусов (это мы уже знаем, так как CHA = OCA) - Ребро CH = √3 (мы только что нашли это значение) Теперь мы можем использовать синус, чтобы найти искомый угол между прямыми MA и BD. Воспользуемся следующей формулой: sin(CHA) = CH / CA Так как мы знаем значения ребра CH (√3) и ребра CA (1), мы можем подставить их в формулу: sin(60 градусов) = √3 / 1 = √3 Таким образом, мы определяем sin(60 градусов) = √3. Теперь мы можем найти искомый угол CHA, взяв обратную функцию синуса: CHA = arcsin(√3) Для получения числового значения данного угла, мы можем воспользоваться калькулятором либо таблицами значений функции arcsin. Итак, угол между прямыми MA и BD в правильной шестиугольной пирамиде MABCDEF, где все ребра равны 1, равен CHA = arcsin(√3). Окончательное значение угла можно найти подставив это выражение в калькулятор или таблицы значений.