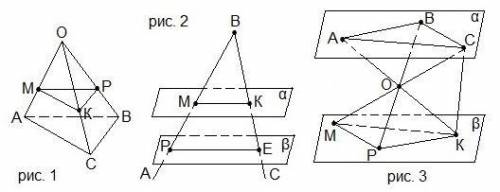
2. На рисунке 1 плоскости АВС и МКР параллельны, АМ:МО=2:5, площадь треугольника МРК равна 50 см2. Найти плоскость треугольника АВС. A) 75 см2; B) 100 см2; C) 96 см2; D) 98 см2.

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е как показано на рисунке 2. Известно, что ВР=3,5МР, ВМ=12,5 см, МК=25 см. Найти РЕ.

A) 35 см; B) 36 см; C) 42 см; D) 34 см.

Все нужно расписать очень подробно, что откуда взялось, использованные теоремы и т.д.

Добрый день! Рассмотрим каждый вопрос по очереди и предоставим ответы с подробным решением.

2. На рисунке 1 плоскости АВС и МКР параллельны, АМ:МО=2:5, площадь треугольника МРК равна 50 см2. Найти площадь треугольника АВС.

Для решения этой задачи, нам потребуется использовать следующие теоремы:

1) Если две плоскости параллельны, то все соответствующие углы между соответствующими сторонами треугольников, образованными этими сторонами, равны.

2) Если отношение длин двух отрезков одно и то же, то соответствующие площади треугольников, образованных этими отрезками, будут иметь такое же отношение.

По условию задачи, АМ:МО=2:5, а площадь треугольника МРК равна 50 см2.

Найдем длину стороны МР в треугольнике МРК:
Для этого возьмем x - наименьший общий множитель чисел 2 и 5, чтобы АМ и МО были целыми числами. Таким образом, АМ=2x, а МО=5x.
Используя отношение сторон треугольников, можно записать следующее уравнение:

(AМ:МО)=(МР:ВС)
(2x:5x)=(МР:ВС)
2:5=МР:ВС
2/5=МР/ВС

Поскольку общая площадь треугольников МРК и АВС равна, и пропорции их сторон также равны, площади этих треугольников будут иметь такое же отношение:
(площадь МРК):(площадь АВС)=2/5.

Теперь, используя это уравнение и площадь треугольника МРК (50 см2), можем найти площадь треугольника АВС:

(50 см2):(площадь АВС)=2/5.

Для определения площади треугольника АВС, умножим обе стороны уравнения на площадь АВС:

площадь АВС=(50 см2)*(5/2).
площадь АВС=250/2.
площадь АВС=125 см2.

Ответ: площадь треугольника АВС равна 125 см2.

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е. Известно, что ВР=3,5МР, ВМ=12,5 см, МК=25 см. Найти РЕ.

Для решения этой задачи, нам потребуется воспользоваться свойствами параллельных прямых и плоскостей и теоремой Пифагора.

Из условия задачи, ВР=3,5МР, ВМ=12,5 см, МК=25 см.

Заметим, что треугольник ВМК - прямоугольный треугольник. Как мы знаем, в прямоугольном треугольнике отношение длин сторон равно отношению длин катетов:

(ВР/МК)=(ВМ/ВР).

Подставив значения из условия задачи, можем записать уравнение:

(3,5МР/25)=(12,5/3,5МР).

Теперь возьмем отношение ВМ/ВР и ВР/МК для дальнейшего решения задачи.

(ВМ/ВР)=(12,5/3,5МР).
(ВР/МК)=(3,5МР/25).

Умножим обе стороны первого уравнения на ВР и обе стороны второго уравнения на МК:

ВМ=(12,5*ВР)/(3,5МР).
ВР=(3,5МР*МК)/25.

Теперь получим уравнение, в котором присутствуют только ВМ и ВР:

ВМ=(12,5*ВР)/(3,5МР) - (1).

ВР=(3,5МР*МК)/25 - (2).

Между уравнениями (1) и (2) существует зависимость: ВР выражено в формуле (2), и это значение можно подставить в формулу (1):

ВМ=(12,5*((3,5МР*МК)/25))/(3,5МР).

Упростим выражение, сокращая 3,5МР в числителе и заключим в скобки выражение (МК/25):

ВМ=(12,5*МК)/(25/МР)).
ВМ=(12,5*МК*МР)/25.

Теперь, чтобы найти РЕ, нам нужно использовать теорему Пифагора для правильного треугольника МРЕ.

ВМ=12,5 см, МК=25 см. Путем использования теоремы Пифагора получим следующее уравнение:

ВЕ^2=ВМ^2-МК^2.

Подставим значения и решим уравнение:

ВЕ^2=12,5^2-25^2.
ВЕ^2=156,25-625.
ВЕ^2=-468,75.

Очевидно, что значением ВЕ не может быть отрицательное число, поэтому данная задача не имеет решения в реальных числах.

Ответ: задача на определение длины РЕ не имеет решения в реальных числах.