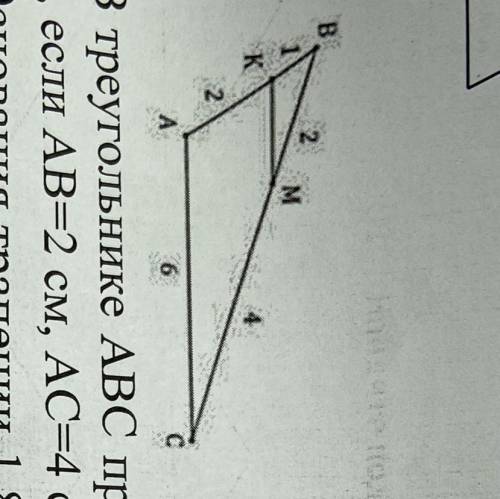
2. Докажите подобие треугольников
АВС и КВМ. Найдите КМ.

Для того чтобы доказать подобие треугольников АВС и КВМ, мы должны проверить выполнение одного из трех условий подобия треугольников: соответствие углов, соответствие сторон или соотношение сторон.

Давайте проверим, выполняется ли условие соответствия углов. Если углы треугольника АВС соответствуют углам треугольника КВМ, то треугольники будут подобными.

На изображении, данном в вопросе, видно, что угол А равен углу К, угол В равен углу М и угол С равен углу В. Из этих равенств мы можем сделать вывод, что углы этих треугольников равны.

Таким образом, условие соответствия углов выполняется и мы можем сделать вывод, что треугольники АВС и КВМ являются подобными.

Теперь, чтобы найти длину КМ, мы можем использовать пропорцию с длинами сторон треугольников АВС и КВМ. Если треугольники подобны, то соотношение длин сторон будет сохраняться.

Из изображения мы можем определить, что отрезок АВ равен 6, отрезок ВС равен 4, а отрезок МВ равен 3.

Теперь составим пропорцию:
(КМ/МВ) = (АС/ВС)

Подставим известные значения:
(КМ/3) = (6/4)

Упростим правую часть:
(КМ/3) = (3/2)

Теперь, чтобы найти КМ, мы можем перекрестно умножить:
2 * КМ = 3 * 3

Упростим уравнение:
2 * КМ = 9

Теперь разделим обе части уравнения на 2:
КМ = 9/2

Получаем, что КМ равно 4.5.

Таким образом, мы доказали подобие треугольников АВС и КВМ и нашли длину КМ, которая равна 4.5.