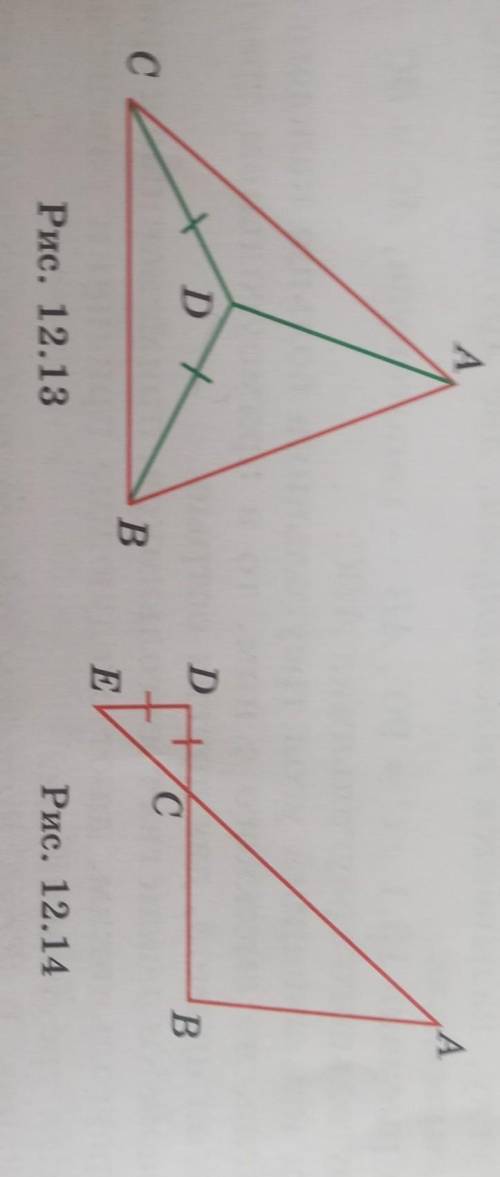
12.18 Вершины треугольника АВС соединены отрезками с точкой D, лежащей внутри этого треугольника, CD = BD, угол ACD меньше угла ABD (рис. 12.13). Докажите, что АС > АВ.
Другие вопросы по теме Геометрия
Популярные вопросы
- В состав океана входят все острова Тихого океана?...
3 - В каких предложениях сказуемые выражены безличными глаголами? Выбери...
3 - Оловянный и латунный шары одинаковой массы, взятые при температуре 23...
3 - Почему раньше писатели писали длинное описание?...
1 - Приведи к несократимой дроби...
3 - До іть будь ласка зробити завдання...
3 - Задание № 3. Вычислите суточную амплитуду температур, если ночью температура...
2 - на примере донецкого края докажите, что экономно-географическое положение...
2 - Абай Кунанбаев 3 карасоз магынасы...
2 - 2) 7/10 : 7 4) 1/100 : 1/100 6) 7 : 1/4 8) 1/5 : 1/10...
3
В треугольнике большая сторона противолежит большему углу. По условию АС >АВ ⇒ угол АВС > угла АСВ. Т.к. CD=BD, треугольник СDВ равнобедренный, и ∠DCB=∠DBC (свойство). . Примем каждый их них равным α. Тогда по основному свойству неравенства АВС-α > АСВ -α, т.е. угол АСD < угла АBD, ч.т.д.