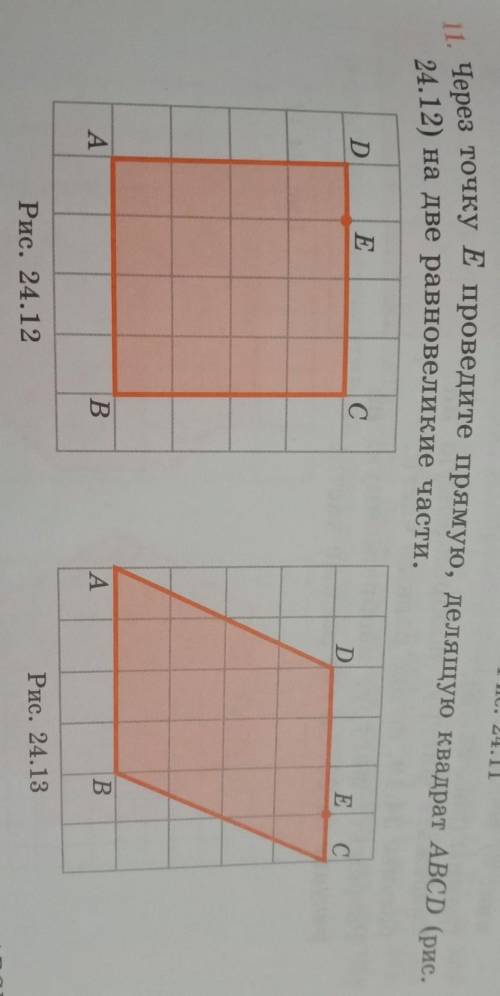
11. Через точку E проведите прямую, делящую квадрат ABCD (рис. 24.12) на две равновеликие части,
​

Для решения этой задачи нам нужно найти такую прямую, которая разделит квадрат ABCD на две равновеликие части.

Давайте рассмотрим данный квадрат ABCD. Мы знаем, что углы в квадрате равны 90 градусов, а стороны равны между собой.

Чтобы найти прямую, которая разделит квадрат на две равновеликие части, мы должны провести ее через точку E.

Чтобы найти такую прямую, мы можем использовать информацию о симметрии квадрата. Мы знаем, что каждая сторона квадрата параллельна противолежащей стороне и равна ей в длине.

Также, мы знаем, что каждая диагональ квадрата делит его на две равновеликие части.

Используя эти знания, давайте проведем прямую через точку E, которая будет параллельна одной из сторон квадрата и также будет проходить через центр квадрата.

Центр квадрата можно найти, соединив противоположные углы квадрата диагоналями. Проведем диагонали AC и BD, и их пересечение будет центром квадрата. Обозначим его точкой O.

Теперь, чтобы провести прямую через центр квадрата, соединим точки O и E с помощью отрезка OE. Таким образом, мы получим прямую, которая будет параллельна стороне AB и делит квадрат на две равновеликие части.

Обоснование:
Мы использовали свойства симметрии квадрата, которые гарантируют, что каждая сторона параллельна противолежащей стороне и равна ей в длине. Мы также использовали свойство диагонали, которая делит квадрат на две равновеликие части.

Пошаговое решение:
1. Соедините точки A и C отрезком AC, и точки B и D отрезком BD.
2. Найдите точку пересечения диагоналей AC и BD и обозначьте ее как точку O.
3. Проведите прямую через точку E и центр квадрата O, используя отрезок OE.

Таким образом, прямая, проведенная через точку E и центр квадрата O, разделит квадрат на две равновеликие части.