10 чертежей на 3 признака равенства треугольников
Что то на подобии такого
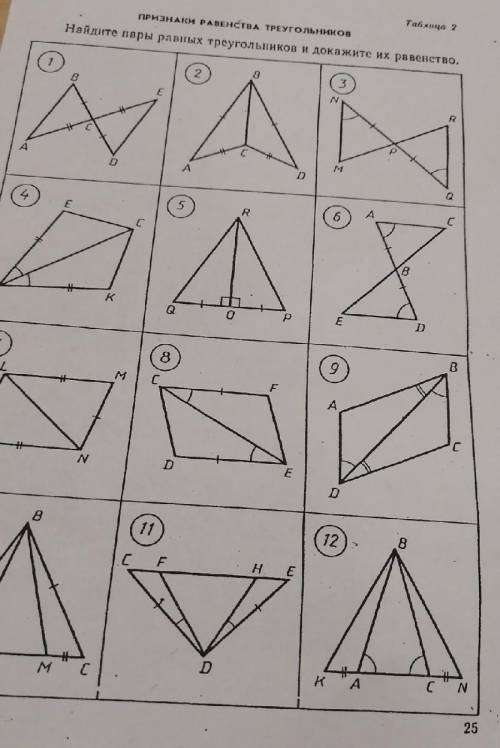
Ответы
Добрый день, ученик! Рад принять роль школьного учителя и помочь вам с решением этой задачи о равенстве треугольников.
Чтобы лучше понять задачу, давайте разберемся в том, что такое признаки равенства треугольников. Признаки – это свойства или условия, которым должны удовлетворять треугольники, чтобы считаться равными. Их всего шесть:
1. Равные стороны
2. Равные углы
3. Равенство двух сторон и угла между ними
4. Равенство двух углов и стороны между ними
5. Равенство трех сторон
6. Равенство всех трех углов
Теперь, основываясь на том, что вы написали про 10 чертежей на 3 признака равенства треугольников и показанный вами чертеж, я позволю себе предположить, что у вас есть 10 треугольников, каждый из которых имеет три признака равенства с другими треугольниками.
Давайте решим эту задачу, чтобы понять, сколько всего различных треугольников имеется в этом наборе. Для этого нам нужно сосчитать комбинации этими 10 треугольниками.
Количество комбинаций можно рассчитать по формуле сочетаний. Формула сочетаний выглядит следующим образом:
C(n, k) = n! / (k! * (n-k)!)
Где n - общее количество треугольников, а k - количество выбранных треугольников для комбинации.
В нашем случае, n=10 (всего 10 треугольников) и k=3 (нам нужно выбрать 3 треугольника для каждой комбинации).
Подставляя значения в формулу, получим:
C(10, 3) = 10! / (3! * (10-3)!)
Давайте посчитаем значение этого выражения:
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3628800
3! = 3 * 2 * 1 = 6
(10-3)! = 7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
Теперь, подставляя значения в формулу, получим:
C(10, 3) = 3628800 / (6 * 5040) = 120
Итак, у нас есть 10 треугольников, и мы можем сформировать 120 различных комбинаций из 3 треугольников каждая.
Надеюсь, это решение помогло вам разобраться в задаче о равенстве треугольников. Если у вас возникнут еще вопросы или потребуется дополнительное объяснение, я всегда готов помочь!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Напиши те предложения со словами рассердился, рассвирепел и разозлился...
2 - Выпишите из текста 2 предложения в страдательном залоге и переведите...
1 - Из слов в скобках составь ответы. где гнездились грачи? (в, березовая,...
3 - Напишите ,что такое маньжурское завоевание китая.мне по ней нужно презентацию...
3 - Даны векторы а (-6: -2) и б (12: 4) найдите координаты вектора 1/2a...
1 - Перечислите меры применяемые для борьбы с заболеваниями которые вызываются...
1 - Сочинение почему в языке появляются неологизмы?...
1 - Сочинение на тему первый зимний день с не саглосованными и не согласованными...
3 - Запиши названия московских улиц в алфавитном порядке.обсудите почему...
3 - Усережи 5 монет по 10 к,а у володи одна монета -50копеек.1)поставь вопрос,чтобы...
3