1)во сколько раз уменьшится площадь боковой поверхности пяти угольной пирамиды, если все рёбра уменьшить в 2 раза, какова будет площадь бок поверхности уменьшен ной пирамиды, если изначально она равна 114?? 2) в правильной четырёхугольной пирамиде P ABCD С ВЕРШИНОЙ Р сторона основания равна 10,боковые ребра равны
Найти площадь поверхности пирамиды PABCD?
3)В правильной треугольной пирамиде P ABC С ВЕРШИНОЙ Р БОК РЁБРА взаимно перпендикулярно и равны 6. Найти площадь бок поверхности РАВС. НАЙТИ ПЛОЩАДЬ ОСНОВАНИЯ ПИРАМИДЫ РАВС
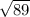
Другие вопросы по теме Геометрия
Популярные вопросы
- Назовите одно любое событие произошедшее в республике дагестан.какое...
3 - Б) после того как цена на игрушки была снижена на 10%, игрушечный...
2 - Может ли выражение 16x+x^2+64 принимать отрицательные значения...
1 - Дізнайтеся яка подія з життя ґая марія зображенна на ілюстрації...
2 - Будь -ласка іть річна контрольна основою світогляду середньовічної...
1 - Ex. ii. продолжите предложения, образовавразделительный вопрос.1....
3 - Вкаждое из данных предложений включите подходящий по смыслу деепричастный...
1 - Реши уравнение 144z+144-z^3-z^2=0...
3 - 1. число начинается на х а заканчивается на y (x y печатается...
2 - Японская война. 2 причинно-следственные связи и 5 фактов....
1
Из данного условия можно сделать два вывода:
- Если все ребра уменьшаются в 2 раза, то периметр основания также уменьшится в 2 раза.
- При данном изменении площадь боковой поверхности пирамиды будет уменьшаться пропорционально изменению периметра основания.
Таким образом, чтобы найти во сколько раз уменьшится площадь боковой поверхности, нужно узнать, во сколько раз уменьшится периметр основания. Из условия известно, что периметр основания равен 114. Если все его ребра уменьшатся в 2 раза, то периметр станет равным 114/2 = 57.
Предыдущий периметр основания равнялся 114, а новый периметр - 57. Значит, площадь боковой поверхности уменьшилась в 114/57 = 2 раза.
Чтобы найти площадь боковой поверхности уменьшенной пирамиды, нужно умножить исходную площадь на коэффициент уменьшения, то есть 114/2 = 57.
Ответ: площадь боковой поверхности уменьшенной пятиугольной пирамиды будет равна 57.
2) Чтобы найти площадь поверхности пирамиды PABCD, нужно найти сумму площадей боковой поверхности и площади основания.
А) Для нахождения площади боковой поверхности нам нужно знать формулу площади боковой поверхности правильной пирамиды с четырехугольным основанием. Данная площадь равна половине произведения периметра основания на высоту боковой грани.
Для нахождения периметра основания пирамиды PABCD нужно сложить длины всех сторон основания: AB + BC + CD + DA = 10 + √(89) + 10 + √(89) = 20 + 2√(89).
Высота боковой грани пирамиды равна расстоянию от вершины P до плоскости ABCD. Данная высота может быть найдена с использованием теоремы Пифагора. Для этого можно рассмотреть треугольник PAD, где AD является гипотенузой, а PH - прямой перпендикуляр от вершины P к плоскости ABCD.
Чтобы найти расстояние PH, нужно воспользоваться формулой для нахождения высоты прямоугольного треугольника: PH = (√(AD^2 - DA^2))/2, где PH - расстояние от вершины P до плоскости ABCD, AD - длина диагонали основания пирамиды PABCD, DA - длина стороны основания пирамиды PABCD.
Длина диагонали основания пирамиды PABCD равна √((√(89))^2 + 10^2) = √89 + 10.
Тогда расстояние PH равно (√((√(89) + 10)^2 - 10^2))/2 = (√(89 + 2√(89) + 100 - 100))/2 = (√(89 + 2√89))/2 = (√89 + √89)/2 = (√89)/2 + (√89)/2 = √89.
Таким образом, высота PR равна √89. По формуле площади боковой поверхности пирамиды, площадь боковой поверхности PAED равна (периметр основания * высоту боковой грани) / 2 = ((20 + 2√(89)) * √89) / 2 = (20√89 + 2√(89^2)) / 2 = (20√89 + 2*89) / 2 = 10√89 + 89.
Б) Для нахождения площади основания пирамиды PABCD нужно знать формулу площади правильного четырехугольного основания, которая равна (сторона основания^2 * √3) / 4.
Площадь основания пирамиды PABCD равна (10^2 * √3) / 4 = 100√3 / 4 = 25√3.
Таким образом, площадь поверхности пирамиды PABCD равна сумме площади боковой поверхности и площади основания: 10√89 + 89 + 25√3.
Ответ: площадь поверхности пирамиды PABCD равна 10√89 + 89 + 25√3.
3) Для нахождения площади боковой поверхности пирамиды PABC нужно знать формулу площади боковой поверхности правильной треугольной пирамиды. Данная площадь равна половине произведения периметра основания на apothem.
Периметр основания треугольной пирамиды равен сумме длин всех сторон основания: AB + BC + CA = 6 + 6 + 6 = 18.
Apothem (ap) - это расстояние от центра основания треугольной пирамиды до середины одной из сторон основания.
Для равностороннего треугольника ap равен (√3 / 6) * длина стороны треугольника.
Таким образом, ap = (√3 / 6) * 6 = (√3) * 1 = √3.
Итак, площадь боковой поверхности пирамиды PABC равна (периметр основания * ap) / 2 = (18 * √3) / 2 = 9√3.
Для нахождения площади основания пирамиды PABC нужно знать формулу площади равностороннего треугольника, которая равна (a^2 * √3) / 4, где a - длина стороны треугольника.
Площадь основания треугольной пирамиды PABC равна (6^2 * √3) / 4 = 36√3 / 4 = 9√3.
Ответ: площадь боковой поверхности пирамиды PABC равна 9√3, а площадь основания равна 9√3.