1. Геометрия
  2. , 1. В прямоугольном треугольнике

, 1. В прямоугольном треугольнике ABC угол С прямой, катеты равны 9 см и 12 см. Найдите косинус и синус угла B.
2. Лестница длиной 15 метров приставлена к вертикальной стене так, что нижний ее коней отстоит от стены на 9 метров. На какой высоте другой конец лестницы?

arave1 arave1    2   23.12.2021 14:58    7

Ответы
Chara05 Chara05  12.02.2022 08:58

1.

\frac{4}{5}

\frac{3}{5}

2. 12м

Объяснение:

1. Найдём гипотенузу АВ по теореме Пифагора:

AB = \sqrt{ {AC}^{2} + {BC}^{2} } = \sqrt{ \ {9}^{2} + {12}^{2} } = \\ = \sqrt{81 + 144} = \sqrt{225} = 15

Далее может быть 2 варианта:

вариант 1: АС=9 см, ВС= 12 см

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.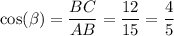

\cos( \beta ) = \dfrac{BC}{AB} = \dfrac{12}{15} = \dfrac{4}{5}

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе

\sin( \beta ) = \dfrac{AC}{AB} = \dfrac{9}{15} = \dfrac{3}{5}

вариант 2: АС=12 см, ВС= 9 см

\cos( \beta ) = \frac{9}{15} = \frac{3}{5} \\ \\ \sin( \beta ) = \frac{12}{15} = \frac{4}{5}

2.

рис.2

В прямоугольном треугольнике АВС(<С=90°), найдём катет АС по теореме Пифагора:

AC = \sqrt{ {AB}^{2} - {BC}^{2} } = \sqrt{ {15}^{2} - {9}^{2} } = \\ = \sqrt{225 - 81} = \sqrt{144} = 12


, 1. В прямоугольном треугольнике ABC угол С прямой, катеты равны 9 см и 12 см. Найдите косинус и си
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Egorpiernand Egorpiernand  08.10.2019 11:01
Дано треугольник abc угол c равен 90 градусов bc биссектриса б а равно 5 см bc равно 3 см найти cd и да​...
Strannik288 Strannik288  08.10.2019 11:01
Найдите высоту параллелограмма, проведенную к его меньшей сторонеесли известны периметр 51см, площадь 90см^2 и меньшая высота 5см​...
djjegsdhssbsv djjegsdhssbsv  08.10.2019 11:01
Найдите высоту прямоугольного треугольника проведённого из прямого угла если она делит основание на отрезки 3 см и 12 см​...
jykov2000 jykov2000  08.10.2019 11:01
Даны прямая и точка, принадлежащая этой прямой.сколько прямых.перпендикулярно данной прямой,можно провести через данную точку?...
GETRRRR GETRRRR  08.10.2019 11:01
Острые углы прямоугольного треугольника относятся как 5: 4. больший из этих углов равен: a). 36 ° б)40° в). 70° г)20°...
verinikamusia verinikamusia  08.10.2019 11:00
Три числа, из которых третье равно 12, образуют убывающую прогрессию. если вместо 12 взять 9, то три числа составят арифметическую прогрессию. найдите первые два...
DeNiSNoNs DeNiSNoNs  08.10.2019 11:00
Зточки зору до прямої проведені дві похилі довжини яких 25см в 17см. знайдіть довжини проекцій цих похилих, якщо вони відносяться як 5: 2...
Aytgbssh Aytgbssh  08.10.2019 11:00
Вправильной пирамиде abcd все ребра равны a,вычислите высоту пирамиды​,решите !...
kolyamusin01 kolyamusin01  08.10.2019 11:00
Із центр о правильного трикутника abc проведено перпендикуляр so до площини трикутника. знайдіть ∆ aso, якшо sc= 8 cм, so= 4 см...
SBusic SBusic  08.10.2019 11:00
There are already too many speculations in that activity. i, in fact, could catch skn renew cream. i don t usually state my personal feelings about things. i had...

Популярные вопросы