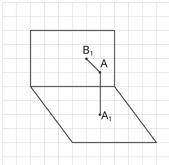
1.В прямом двугранном угле дана точка A. Расстояния от точки A до граней угла: AA1=6 см и AB1=8 см. Определите расстояние от точки A до ребра двухгранного угла с решением
Другие вопросы по теме Геометрия
Популярные вопросы
- Назовите образования слова важнейший...
2 - Від слів утворених написати якомога більше нових слів використовуючи різн словотворення...
2 - 1)в каком выражении используются слова научного стиля? драгоценный камень,грамматическая...
2 - Как из семи пятерок получить ответ 1005...
1 - Трава при сушке теряет 88% своей массы.сколько свежей травы надо скосить чтобы...
2 - Как выглядела герда в начале сказки? (по характеру)...
2 - Блокнот коштуе 8 грн що становить восьму частину вартості книжки. скільки грошей...
2 - Объясните, почему казаков назвал свой рассказ тихое утро (смысл названия)...
2 - (2a+b)^2-(2a-3b)(3b+2a) и решить при а =2, при b=1: 5...
3 - Найдите значение выражения 5-1 1/2 * 1,2...
2
Для начала, давайте посмотрим на то, как угол ABC расположен относительно точки A. Мы видим, что расстояние от точки A до грани BC обозначено как AB1 = 8 см, а расстояние от точки A до грани AC обозначено как AA1 = 6 см.
Теперь, давайте представим, что мы проводим перпендикуляр из точки A на ребро BC. Обозначим точку пересечения перпендикуляра с ребром BC как D. Получается, что расстояние от точки A до ребра BC будет равно расстоянию AD.
Заметим, что треугольник ADB является прямоугольным треугольником, так как перпендикуляр, проведенный из точки A, образует прямой угол с ребром BC.
Теперь, чтобы найти расстояние AD, мы можем воспользоваться теоремой Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы (в данном случае AD) равен сумме квадратов катетов (в данном случае AB1 и AA1).
Таким образом, мы можем записать уравнение следующим образом:
AD^2 = AB1^2 + AA1^2
Вставляя известные значения, получаем:
AD^2 = 8^2 + 6^2
AD^2 = 64 + 36
AD^2 = 100
Чтобы найти значение AD, мы должны извлечь квадратный корень из обеих сторон уравнения:
AD = √100
AD = 10
Таким образом, расстояние от точки A до ребра двугранного угла равно 10 см.
Ответ: Расстояние от точки A до ребра двугранного угла равно 10 см.