№1. стороны двух квадратов равны 8 см и 15 см. найдите сторону квадрата, площадь которого равна сумме площадей данных квадратов. № 2. на стороне аd прямоугольника abcd постройте треугольник аdе так, чтобы точка пересечения отрезков вс и ав была серединой стороны ае. докажите, что площадь прямоугольника abcd равна площади треугольника aed
Другие вопросы по теме Геометрия
Популярные вопросы
- Назовите средства художественной выразительности в стихотворении Н. Рубцова...
3 - У поданому уривку визначте художні тропи: вітерець тихесенько гойдає, майнула...
2 - Если направление силы совпадает с направлением движения тела, то данная...
2 - Поява і розвиток рослинних угроповань у місцеіснуваннях, де рослинності...
1 - Визначити та записати тему, основну думку та конфлікт твору Чайка Джонатан...
2 - При взаємодії калій карбонату з кальцій хлоридом утворюється калій хлорид...
3 - решить (4х-3)(4х+3)-(4х-1)2=3х...
2 - Очень нужно В трех пробирках без этикеток содержатся жидкости: хлорид на...
3 - Тихий і ласкавий на весні бе(з,с)турботний неяскравий вечір. Ні стомлюючої...
3 - Характеристика Тихого океана за планом:...
1
1)
найдём площади обоих квадратов
8*8=64
15*15=225
64+225=289
V289=17
ОТВЕТ: 17
2 не знаю, прости...
№1
S1=8*8=64
S2=15*15=225
S3=225+64=289
сторона третьего квадрата =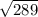 = 17см.
= 17см.
№2.
Е
В О С
А Д
Что бы доказать, что площадь прямоугольника ABCД равна площади треугольника AEД, надо доказать, что площадь треугольника ЕВО=площади треугольникаОСД (т.е. треугольники равны), т.к. пдощадь АВСД=площадьАВОД+площадьОСД.
АВ=ВЕ (по построению)
АВ=СД (по св-вам прямоугольника)
следовательно ВЕ=СД
уголОЕВ=углуСДО (т.к. накрест лежащие для АЕ II СД и секущей ЕД)
угол ОСД=углуЕВО=90градусов
следовательно тр.ВЕО=тр.ОСД по стороне и двум прилежащим углам (по II признаку)
Что и требовалось доказать.