1)сторона правильного шестиугольника, вписанного в окружность, равна 20. в ту же окружность вписан квадрат. чему равна площадь круга, вписанного в этот квадрат? 2)найдите сторону правильного шестиугольника, описанного около
окружности радиуса r. 3)чему равен угол между двумя диагоналями, проведенными из одной вершины правильного пятиугольника. )

№1.

R - радиус описанной окружности, r - радиус окружности, вписанной в квадрат, а - сторона правильного шестиугольника, х - сторона квадрата, S - площадь круга.

R=a=20

ответ: площадь круга, вписанного в квадрат, 628.

№2.

а - сторона правильного шестиугольника

ответ: сторона правильного шестиугольника .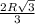

№3.

Каждый из пяти углов правильного пятиугольника равен

.

Если провести две диагонали из одного угла, то они разделят пятиугольник на три треугольника. Рассмотрим два треугольника, в которых две из сторон являются сторонами исходного пятиугольника. Эти треугольники равны по первому признаку равенства треугольников, кроме того, они оба равнобедренные. Величина равных углов равна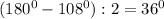 . Угол между диагоналями будет равен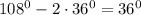

ответ: угол между двумя диагоналями, проведенными из одной вершины правильного пятиугольника, равен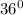 .