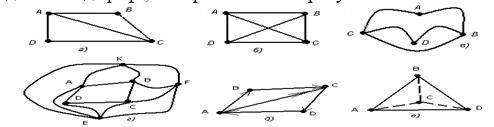
1. Определите вид графа, изображенного на рисунке.

2. Определите по рисунку первого задания, сколько каждый граф имеет всего: а) вершин; б) ребер; в) граней, считая и внешнюю грань; г) нечетных вершин; д) четных вершин; е) вершин, со степенью равной 0.
а) вершин; б) ребер; в) граней, считая и внешнюю грань; г) нечетных вершин; д) четных вершин; е) вершин, со степенью равной 0.

3. Определите по рисунку первого задания, какой граф можно начертить одним росчерком (без отрыва карандаша от бумаги и без повторения движения по каждому из ребер).

4. Сформулируйте и докажите терему о свойстве любого графа.

5. Через реку Прегель, протекающую по городу Кенигсберг (Калининград) было построено 7 мостов, которых связывали его берега с двумя островами, расположенными в черте города (как на рисунке). Можно ли пройти по всем мостам так, чтобы на каждом из них побывать лишь один раз и вернуться к тому месту, откуда начнешь прогулку.

Решая эту задачу «о семи мостах» Л. Эйлер поступил седеющим образом. Он изобразил точками В и С берега реки, точками А и D острова, а линиями – мосты, соединяющие соответствующие участки берегов и островов. Изобразите граф,

соответствующий этой задаче и объясните, как решил задачу Л. Эйлер.

bocmanlera    2   19.10.2020 06:13    18