1. Найти площадь треугольника, если его стороны 4 и 7 см, а угол между ними 30 градусов. 2. Найти площадь ромба, сторона которого равна 5 корней из 3 см, а один из углов 150 градусов.
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите сочинение на тему: осень...
3 - 1)как вы понимаете информацию о том, что масштаб карты равен 1: 100000?...
2 - Y=kx-3 проходит через точку а(-2; 9)...
1 - Fill in the where necessary1. kremlin 2. red square 3. piccadilly...
1 - Как сопоставить слово яблокопад со словами листопад,звездопад...
1 - Фонетический разбор слова деревья...
3 - Проверочное слово к слову транскрипция...
2 - Сочинение рассуждение на тему почему александр невский воплощение...
1 - Решение по действиям ((27,12+43,08)*0,007-0,0314)*100=...
2 - Перевидите и поставьте пропущено е слова the teacher turned the lamb...
3
Задача 1 - ответ: 7 см².
Задача 2 - ответ: 37,5 см².
Объяснение:
Задача 1.
Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними:
S = (4*7*sin30°) :2 = (28*0,5) : 2 = 7 см².
ответ: 7 см².
Задача 2.
Сумма углов ромба, прилегающих к одной его стороне, равна 180°. Поэтому если один угол равен 150°, то второй угол равен 30°.
Так как ромб состоит из двух равновеликих треугольников, то его площадь можно выразить как удвоенное произведение площади одного треугольника, равную половине произведения двух сторон ромба на синус угла между ними:
S = [(5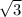 * 5
* 5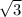 *sin30°) :2] * 2 = 5
*sin30°) :2] * 2 = 5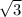 * 5
* 5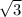 *sin30° = 25*3*0,5 = 37,5 см².
*sin30° = 25*3*0,5 = 37,5 см².
ответ: 37,5 см².