1. Хорды AB и CD окружности пересекаются в точке K. Найдите BK , если AK= 8, KD=4, CK=6 2. Задача на фото
3. Задача на фото

Добрый день! Давайте решим поставленные задачи по порядку.

1. Дано: Хорды AB и CD окружности пересекаются в точке K. Значения AK = 8, KD = 4 и CK = 6. Требуется найти значение BK.

Для начала, нам необходимо понять, как связаны хорды AB, CD и их пересечение в точке K. Заметим, что хорды AB и CD делятся точкой K на две части. Обозначим эти части как x и y.

Так как хорды AB и CD пересекаются в точке K, то согласно теореме о внутрихордовых углах (теорема секущей), x*y = AK * KB = CK * KD.

В нашем случае x = AK и y = KB. Поэтому, мы можем записать равенство следующим образом: AK * KB = CK * KD.

Подставим известные значения: 8 * KB = 6 * 4.

Далее, решим полученное равенство относительно KB:

8 * KB = 24.

Чтобы найти значение KB, разделим обе части равенства на 8:

KB = 24 / 8 = 3.

Таким образом, мы нашли значение BK, оно равно 3.

2. Перейдем ко второй задаче.

На фотографии изображен треугольник ABC, прямоугольник EFGH и окружность с центром в точке O. А также дано, что AB является касательной к окружности в точке B, AC является касательной к окружности в точке C, и AD является диаметром окружности.

Требуется найти угол BAE.

Поскольку прямоугольник EFGH является касательной AB, то угол BAD противоположный углу EAF.

Так как AD является диаметром окружности, угол BAD - прямой угол.

Это означает, что угол EAF также равен прямому углу, то есть 90 градусов.

Угол BAE - это тот же угол, что и угол EAF.

Поэтому, угол BAE также равен 90 градусов.

Ответ: угол BAE равен 90 градусов.

3. Перейдем к третьей задаче.

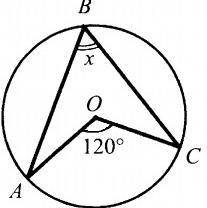
На фотографии изображен треугольник ABC, окружность с центром в точке O и точка D на окружности.

Требуется найти угол ABC.

Для решения этой задачи, воспользуемся теоремой о вписанных углах: угол, опирающийся на дугу, равен половине угла центра, опирающегося на ту же дугу.

Так как точка D лежит на окружности с центром в точке O, угол DOC является центральным углом.

Согласно теореме о вписанных углах, угол ABC будет равен половине угла DOC.

Угол DOC равен 140 градусам (так как это центральный угол и он равен удвоенному углу на окружности, опирающемуся на ту же дугу).

Половина угла DOC равна 70 градусам.

Ответ: угол ABC равен 70 градусам.