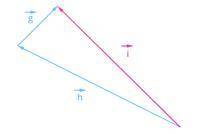
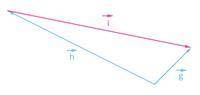
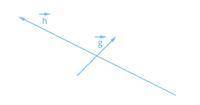
1 Даны векторы g→ и h→. На каком из данных рисунков построена разность векторов g→ и h→, т. е. вектор g→−h→?
а1
б2
в3
г4

Другие вопросы по теме Геометрия
Популярные вопросы
- Лексическое значение и как появились слова фонетика орфоэпия лингвистика...
1 - Будут ли реагировать разбавленные серная и соляная кислоты со следующими...
3 - Нужно сочинение на тему должны ли дети воевать?...
3 - Abc равнобедренный треугольник ав=вс=17 вн-высота вн=15 ас?...
3 - Уравнение х+(34+17)=80 .(50-17)+у=70 ....
2 - The royal mail a) collects and delivers letters. b) collects letters....
3 - Чему равна площадь квадрата со стороной 9дм 9см 9м...
3 - Надо изобразить квантовые ячейки кремния. заранее !...
2 - Кусок льда весом 10 н плавает в воде, объем вытесненной льдом воды...
3 - Какое количество вещества содержится в 345 г платины?...
1
1. Найдите разность координат векторов g→ и h→ по каждой оси. Для этого вычитаем из каждой координаты g→ соответствующую координату h→:
g→ - h→ = (g_x - h_x, g_y - h_y)
2. После нахождения разности координат, нужно построить новый вектор с этими разностями координат.
Теперь посмотрим на каждый из рисунков:
а1:
Этот рисунок не подходит, так как векторы g→ и h→ не соответствуют осям x и y. Мы можем увидеть, что g→ направлен вниз, а h→ направлен вправо.
б2:
Этот рисунок также не подходит, так как векторы g→ и h→ не соответствуют осям x и y. Мы можем увидеть, что g→ направлен вниз, а h→ направлен вверх.
в3:
Этот рисунок подходит, так как векторы g→ и h→ соответствуют осям x и y. Мы можем увидеть, что g→ направлен вниз, а h→ направлен влево. Разность векторов g→ и h→ будет иметь следующие координаты: (-3, 2).
г4:
Этот рисунок также не подходит, так как векторы g→ и h→ не соответствуют осям x и y. Мы можем увидеть, что g→ направлен влево, а h→ направлен вправо.
Таким образом, разность векторов g→ и h→ построена на рисунке в3.