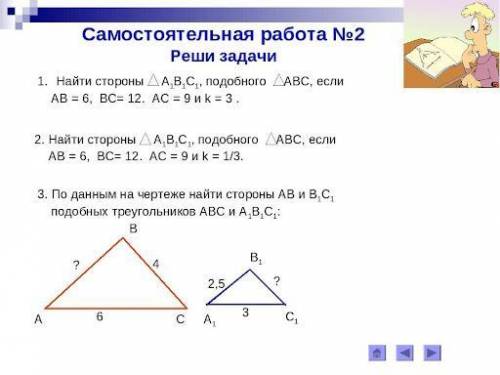
1 Дано треугольник АБС подобен треугольнику А1Б1С1. БС=4 АС=6 А1Б1=2.5 А1С1=3 Найти стороны АБ и Б1С1

АСА1= вроде правильно
579

Для решения данной задачи, можно воспользоваться свойством подобных треугольников, согласно которому соответствующие стороны подобных треугольников имеют одно и то же отношение.

Итак, у нас есть данные следующих отрезков:

BC = 4, AC = 6, A1B1 = 2.5 и A1C1 = 3.

Мы хотим найти длины сторон AB и B1C1.

Сначала, найдем соотношение между сторонами треугольников АБС и А1B1С1. Для этого, возьмем отношение сторон АС и A1С1.

AC / A1C1 = 6 / 3 = 2

Теперь, мы знаем, что отношение сторон АС и A1С1 равно 2.

Затем, можно найти соотношение между сторонами AB и A1B1. Для этого, возьмем отношение сторон BC и B1C1.

BC / B1C1 = 4 / x, где x - длина стороны B1C1, которую мы хотим найти.

Теперь, мы знаем, что отношение сторон BC и B1C1 равно 4 / x.

Также, мы знаем, что отношение сторон AB и A1B1 равно 2.

Теперь мы можем записать соотношения:

BC / B1C1 = 4 / x = 2

2x = 4

x = 4 / 2

x = 2

Таким образом, сторона B1C1 равна 2.

Теперь, найдем сторону AB. Для этого, умножим значение А1B1 на отношение сторон АС и A1С1.

AB = A1B1 * (AC / A1C1)

AB = 2.5 * (6 / 3)

AB = 2.5 * 2

AB = 5

Таким образом, сторона AB равна 5.

Итак, мы получили, что AB = 5 и B1C1 = 2.