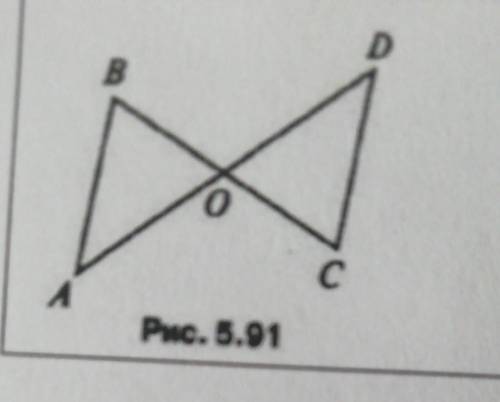
1. Дано: AB = CD, угол ABC = 65°, угол ADC = 45°, угол AOC = 110° (рис. 5.91). Найти: угол C. Доказать: треугольник АВО= треугольнику

Для начала докажем, что треугольник АВО равен треугольнику СОD.

Из дано: AB = CD (1)
Угол ABC = 65° (2)
Угол ADC = 45° (3)
Угол AOC = 110° (4)

Так как угол ABC = угол ADC, зная (2) и (3), мы можем сделать вывод, что треугольник ABC равен треугольнику ADC по двум сторонам и углу, что позволяет нам утверждать, что AB = CD (по принципу равенства треугольников по двум сторонам и углу). Из (1) и (2) следует, что треугольники АВС и CDE равны по двум сторонам и углу, поэтому можем утверждать, что угол B = углу D.

Так как углы треугольника суммируются в 180°, мы можем найти угол C, используя углы треугольника AOC.

Угол AOC = 180° - угол OCA - угол OAC.
Угол OCA = угол ABC = 65° (из (2))
Угол OAC = угол C + угол OCA (из (4))
= угол C + 65°

Подставляем известные значения:
110° = 180° - (угол C + 65°)

Упрощаем уравнение:
45° = угол C + 65°

Вычитаем 65° с обеих сторон:
45° - 65° = угол C

-20° = угол C

Таким образом, угол C равен -20°.