1)Дан треугольник со сторонами 20 см, 34 см и 42 см.Данная точка P находится на расстоянии 25 см от всех сторон треугольника. Найти расстояние от точки P до плоскости треугольника. 2)Дан треугольник со сторонами 39 см ,17 см ,28 см. Точка S находится на расстоянии 6 см от плоскости треугольника и на одинаковом расстоянии от его вершин.Найдите расстояние от S до вершин треугольника.
РЕШИТЬ ХОТЬ 1 ЗАДАЧУ
Другие вопросы по теме Геометрия
Популярные вопросы
- Что такое университет в европе и в россии?...
2 - Укажите характерную черту развития культуры в период «застоя». 1)отмена цензуры...
3 - Скільки цілих чисел розшташовано на координатній прямій між числами -3 і...
2 - 1.какой объем занимает 4 моль кислорода o2? 2.масса метана ch4 равна 80 г.чему...
1 - 5. определите объект, координаты которого: 3 градуса ю.ш., 38 градусов в.д....
2 - Найдите наибольшее значение функции y=-18x^2+36 x+1. ! желательно с решением....
1 - Напишите электронный a)o2+2na2so3=2na2so4 б)2fecl3+2kl=2fecl2+i2+2kcl...
3 - 2.на каком основании лес считают ценнейшим экологическим фактором?...
3 - 1. найдите предложения, в которых слово просто является наречием. выпишите...
2 - Площадь участка 156 м² ширина 12 см.чему равна длина участка....
3
24 см
Объяснение:
1) Пусть РО - расстояние от точки Р до плоскости (т.О ∈ плоскости, РО - высота пирамиды). Поскольку точка P находится на расстоянии 25 см от всех сторон треугольника, то т. О - центр круга, впис. в треугольник (r).
р=(20+34+42)/2=48
по формуле Герона S =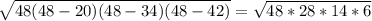 =
= cм²
cм²
r=S/p, r=336/48= 7 см
За т. Пифагора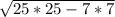 =
=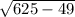 =24 см
=24 см
2) Поскольку т. S находится на одинаковом расстоянии от вершин треугольника, то т.О - центр круга, опис. навк.треугольника.
Далее аналогично: найти р = 42 , потом S по формуле Герона (S = 210), а потом найти R = 39*28*17/4*210=22,1
Далее использовать т. Пифагора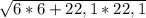 =22,9
=22,9