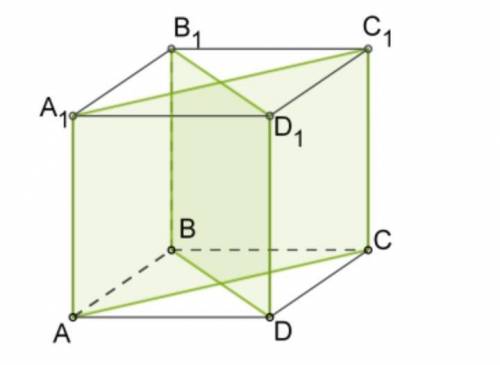
1. Дан куб. Определи, какая из данных в ответе прямых перпендикулярна данной плоскости? а) Плоскости (ABC) перпендикулярна прямая

BD1

AC1

AC

AA1

AB

BD

B1C1

б) Плоскости (ACC1) перпендикулярна прямая

BD1

B1C1

AA1

AC

AC1

BD

AB

2. В какой ситуации проведённая прямая, которая не лежит в плоскости названной фигуры, перпендикулярна плоскости этой фигуры?

1) Прямая проведена перпендикулярно двум диаметрам окружности

2) Прямая проведена перпендикулярно основаниям трапеции

2) Прямая проведена перпендикулярно сторонам ромба с общей вершиной

3) Прямая проведена перпендикулярно двум сторонам параллелограмма

4) Прямая проведена перпендикулярно диагоналям прямоугольника

1. Для определения, какая из данных прямых перпендикулярна плоскости (ABC), мы должны учитывать следующие факты:

- Плоскость (ABC) будет перпендикулярной прямой BD1, если BD1 будет пересекать (ABC) под прямым углом. Чтобы это проверить, можем провести воображаемую линию и убедиться, что она будет перпендикулярна плоскости. Если это не так, мы можем исключить этот вариант.

- Плоскость (ABC) будет перпендикулярной прямой AC1, если AC1 будет пересекать (ABC) под прямым углом. Повторяем тот же процесс, чтобы проверить это. Если AC1 не перпендикулярна, мы отбрасываем этот вариант.

- Продолжаем повторять такой же процесс для всех остальных прямых. В результате мы должны получить единственный вариант, который будет перпендикулярен плоскости (ABC).

2. Для определения, в какой ситуации проведенная прямая будет перпендикулярна плоскости фигуры, мы должны рассмотреть каждую ситуацию:

- Прямая, проведенная перпендикулярно двум диаметрам окружности, будет перпендикулярна плоскости окружности, так как диаметры пересекаются под прямым углом.

- Прямая, проведенная перпендикулярно основаниям трапеции, не будет перпендикулярна плоскости трапеции, так как она не будет пересекать трапецию под прямым углом.

- Прямая, проведенная перпендикулярно сторонам ромба с общей вершиной, будет перпендикулярна плоскости ромба, так как стороны ромба пересекаются под прямым углом.

- Прямая, проведенная перпендикулярно двум сторонам параллелограмма, не будет перпендикулярна плоскости параллелограмма, так как она не будет пересекать параллелограмм под прямым углом.

- Прямая, проведенная перпендикулярно диагоналям прямоугольника, будет перпендикулярна плоскости прямоугольника, так как диагонали пересекаются под прямым углом.

В результате проведения такого анализа, мы можем определить, в каких ситуациях проведенная прямая будет перпендикулярна плоскости соответствующей фигуры.