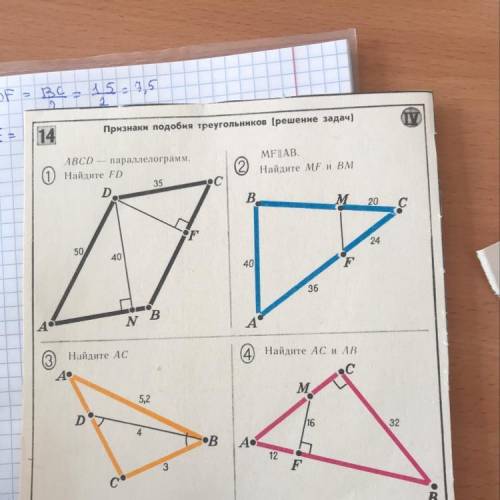
1. ABCD - параллелограмм. Найдите FD. 2. MG||AB. Найдите MF и BM
3. Найдите AC
4. Найдите AC и AB

признаки подобия треугольников

Добрый день! Давайте рассмотрим каждый вопрос по порядку.

1. В данном случае у нас есть параллелограмм ABCD.

Для нахождения длины отрезка FD, нам потребуется использовать свойство параллелограмма, которое гласит: "Диагонали параллелограмма делятся пополам и взаимно перпендикулярны". Используя данное свойство, мы можем сказать, что отрезок FD равен половине диагонали AC. Таким образом, нам нужно найти длину диагонали AC и разделить ее на 2.

2. В данном случае у нас дано, что прямая MG параллельна стороне AB.

Для нахождения длин отрезков MF и BM, мы можем воспользоваться теоремой о параллельных прямых, которая гласит: "Если две прямые параллельны, то отрезки, проведенные перпендикулярно к этим прямым из одной точки, пропорциональны".

Переведя данное выражение на нашу задачу, мы можем сказать, что отрезок MF будет пропорционален отрезку AB, а отрезок BM будет пропорционален отрезку MG. Мы можем использовать пропорциональность для нахождения отрезков MF и BM. Для этого нам потребуется знать длину отрезка AB и длину отрезка MG.

3. Для нахождения длины отрезка AC, нам нужно воспользоваться теоремой Пифагора, которая гласит: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов". В нашем случае, треугольник ABC является прямоугольным, поскольку одна его сторона является диагональю параллелограмма. Таким образом, мы можем использовать теорему Пифагора для нахождения длины отрезка AC.

4. Для нахождения длин отрезков AC и AB, нам также пригодится теорема Пифагора. В данном случае, нам нужно найти длины сторон параллелограмма ABCD, поскольку эти стороны являются диагоналями треугольника ABC. Мы можем использовать теорему Пифагора для каждой из этих диагоналей.

Теперь давайте решим каждый вопрос по порядку, используя данные показанные на рисунке.

1. Для того чтобы найти длину отрезка FD, нам потребуется найти длину диагонали AC. На рисунке дана длина отрезка AB, которая равна 8 см. Поскольку ABCD - параллелограмм, то значит стороны AB и CD равны. Таким образом, длина отрезка CD также будет 8 см. Теперь нам нужно найти длину отрезка AC, который является диагональю параллелограмма ABCD. Для этого нам нужно воспользоваться теоремой Пифагора в треугольнике ABC. Мы имеем AB = 8 см, BC = 6 см. Применяем теорему Пифагора: AC^2 = AB^2 + BC^2. Подставляем значения: AC^2 = 8^2 + 6^2. Производим вычисления: AC^2 = 64 + 36 = 100. Для нахождения AC нужно взять квадратный корень из 100: AC = √100 = 10. Теперь известна длина диагонали AC. Нам нужно найти длину отрезка FD, который равен половине длины диагонали AC. FD = AC/2 = 10/2 = 5.

2. Для нахождения длин отрезков MF и BM, мы можем использовать свойство пропорциональности отрезков, проведенных перпендикулярно к параллельным прямым из одной точки. Мы знаем, что MG || AB. В этом случае отрезки MF и AB будут пропорциональны, а отрезки BM и MG будут пропорциональны. На рисунке дана длина отрезка AB, которая равна 8 см. Нам нужно найти длину отрезка MF. Для этого мы построим прямую, параллельную AB и пересекающую прямую MC. Поскольку прямая MG || AB, она же будет параллельна новой прямой, которая пересекает MC. Таким образом, отрезок MF также будет пропорционален отрезку AB. Зная длину отрезка AB, мы можем использовать пропорциональность для нахождения длины отрезка MF. Аналогично, нам нужно найти длину отрезка BM, который будет пропорционален отрезку MG. На рисунке дана длина отрезка MG, которая равна 4 см. Мы можем использовать пропорциональность для нахождения длины отрезка BM. Таким образом, нам требуется знать длины отрезков AB и MG, чтобы найти длины отрезков MF и BM.

3. Для нахождения длины отрезка AC, нам нужно воспользоваться теоремой Пифагора в прямоугольном треугольнике ABC. На рисунке даны длины сторон AB = 8 см и BC = 6 см. Применяем теорему Пифагора: AC^2 = AB^2 + BC^2. Подставляем значения: AC^2 = 8^2 + 6^2. Производим вычисления: AC^2 = 64 + 36 = 100. Для нахождения длины отрезка AC нужно извлечь квадратный корень из 100: AC = √100 = 10.

4. Для нахождения длин отрезков AC и AB, мы также можем воспользоваться теоремой Пифагора. В этом случае нам нужно найти длины диагоналей параллелограмма ABCD. На рисунке даны длины сторон AB = 8 см и BC = 6 см. Применяем теорему Пифагора: AC^2 = AB^2 + BC^2. Подставляем значения: AC^2 = 8^2 + 6^2. Производим вычисления: AC^2 = 64 + 36 = 100. Для нахождения длины отрезка AC нужно извлечь квадратный корень из 100: AC = √100 = 10.

Надеюсь, эти пояснения помогли вам понять, как найти ответы на каждый из данных вопросов. Если у вас возникнут еще какие-либо вопросы, не стесняйтесь задавать их!