1.14. Точка M равноудалена от всех прямых, содержащих стороны пра- вильного треугольника ABC. Проекцией точки М на плоскость ABC
является точка О, принадлежащая треугольнику. Найдите расстояние
от точки M до стороны AB, если расстояние от этой точки до плоско-
сти ABC равно
AB = 18 см.
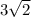
Другие вопросы по теме Геометрия
Популярные вопросы
- с решением (3 2/3 + 2 1/7 × 2 1/10)÷(4 1/3 - 3 35/60)= и вот этот (3 1/4 + 2 1/6)÷...
3 - Сенкан про загадки на русском...
3 - Какие пословицы и поговорки вы хотели бы использо- вать в своей разговорной речи?...
1 - Коли виконували русальні пісні...
3 - Найти предел х/sin (14x) при х стремится к бесконечности...
1 - 4. Найдите в тексте английские эквиваленты следующих словосочетаний: Функциональный...
1 - Составь карту событий об одном из 12 подвигов геракла...
1 - Бубьласка до іть! Виписати всі художні засоби з пісні Гомін, гомін по діброві...
2 - Complete the sentences with the correct from of have got помагити...
2 - В арифметической прогрессии найдите S40-S20 если а21=65, d=3...
2
Из условия задачи становится понятно, что точка M находится на перпендикуляре, опущенном из O на плоскость ABC. При этом, так как треугольник ABC является равносторонним, то перпендикуляры, опущенные из разных вершин треугольника на противоположные стороны, являются высотами треугольника и пересекаются в одной точке - точке пересечения высот, которую мы обозначим как H.
Так как точка M находится на перпендикуляре опущенном из O, то расстояние от точки M до плоскости ABC равно высоте треугольника, опущенной из точки H.
Известно что:
AB = 18 см.
Расстояние от точки M до плоскости ABC равно 3√2 см.
Для решения задачи требуется найти расстояние от точки M до стороны AB треугольника ABC.
Для этого, нам необходимо найти высоту треугольника, опущенную из точки H, на сторону AB.
Обратимся к прямоугольному треугольнику AHM. Этот треугольник образован перпендикулярами к сторонам AB и AC.
Расстояние от точки M до стороны AB треугольника ABC будет равно высоте треугольника AHM, опущенной на сторону AB.
Чтобы найти это значение, нам нужно знать длину стороны AH и площадь треугольника ABC.
К счастью, у нас есть все необходимые данные. Мы знаем, что треугольник ABC является равносторонним. Значит, высота треугольника AHM параллельна стороне AC и делит ее на две равные части.
Можно использовать формулу площади треугольника: S = (1/2) * AC * h, где S - площадь треугольника, AC - длина стороны, h - высота треугольника. Заметим, что S также является площадью треугольника ABC.
Разберемся с площадью треугольника ABC. Известно, что треугольник ABC - равносторонний. Его площадь можно найти по формуле: S = (sqrt(3)/4) * AB^2.
Подставим известные значения в эту формулу:
S = (sqrt(3)/4) * (18^2) = (sqrt(3)/4) * 324 = (81sqrt(3))/2.
Так как высота треугольника AHM делит сторону AC на две равные части, то AC = 2 * AH.
Теперь подставим значения площади S и длины стороны AC в формулу площади треугольника: S = (1/2) * AC * h. Подставим значение вычисленной площади S, длины стороны AC и неизвестное значение h в эту формулу.
(81sqrt(3))/2 = (1/2) * (2 * AH) * h.
Упростим выражение:
(81sqrt(3))/2 = AH * h.
Заметим, что AH * h - это площадь треугольника AHM, значит AH * h = (1/2) * 18 * h.
Теперь мы имеем равенство:
(81sqrt(3))/2 = (1/2) * 18 * h.
Упростим это выражение:
(81sqrt(3))/2 = 9h.
Для решения этого уравнения относительно h, мы можем разделить обе части на 9.
9h = (81sqrt(3))/2.
Теперь нам необходимо выразить h. Для этого мы разделим обе части на 9.
h = (81sqrt(3))/18 = 9sqrt(3)/2.
Таким образом, мы получаем, что высота треугольника AHM равна (9sqrt(3))/2 см.
Теперь мы знаем длину стороны AH и высоту треугольника AHM. Мы можем использовать теорему Пифагора, чтобы найти расстояние от точки M до стороны AB треугольника ABC.
Согласно теореме Пифагора, в прямоугольном треугольнике, квадрат гипотенузы (в данном случае, стороны AB) равен сумме квадратов катетов (в данном случае, стороны AH и расстояния от точки M до стороны AB).
Применим эту формулу. Пусть d - расстояние от точки M до стороны AB. Тогда для треугольника AHM, верно следующее:
d^2 + (9sqrt(3)/2)^2 = 18^2.
Упростим это выражение:
d^2 + (81/4 * 3/2) = 18^2.
d^2 + (81/8) = 18^2.
d^2 + 81/8 = 324.
d^2 = 324 - 81/8.
d^2 = (2592 - 81)/8.
d^2 = 2511/8.
Теперь найдем корень из обеих сторон уравнения:
d = sqrt(2511/8) ≈ 7.812.
Таким образом, расстояние от точки M до стороны AB треугольника ABC составляет примерно 7.812 см.