Заряд на обкладках конденсатора изменяется с течением времени по закону q(t) = 4*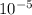 cos4πt (Кл). Чему равна фаза колебаний заряда спустя 5с после начала колебаний?
cos4πt (Кл). Чему равна фаза колебаний заряда спустя 5с после начала колебаний?
Другие вопросы по теме Физика
Популярные вопросы
- ответьте на вопросы с переводом Wie viele Jahreszeiten hat das Jahr?...
2 - Отличия ручного,ножного и электрического привода в швейной машине....
3 - Порівняйте зображення готичних дерев яних церков на Закарпатті з...
2 - тез арада комектесиндерши...
3 - сделайте сами не берите с других источников...
1 - Вычислите значение выражения √(-5)2+√4...
2 - После увеличения абсолютной температуры от 300К до 360K объем газа...
1 - составить рассказ 《книга-мой лучший друг нужно...
1 - Определи верный ответ. Впервые применил прививку И. Мечников Р....
1 - Позначте речовини немолекулярної будови: А)S8 і O2Б) Fe і NaClВ)Co...
2
Изначально у нас задано уравнение q(t) = 4 * 10^(-5) * cos(4πt), где q(t) - заряд на обкладках конденсатора в момент времени t.
Подставляем t = 5 в уравнение:
q(5) = 4 * 10^(-5) * cos(4π * 5)
= 4 * 10^(-5) * cos(20π)
Теперь наша задача вычислить cos(20π).
Для этого воспользуемся формулой полного косинуса:
cos(2πn + φ) = cos(φ)
В данном случае φ = 20π = 2π * 10.
Так как cos(2π) = 1, то cos(20π) = cos(2π * 10 + 0) = cos(0) = 1.
Итак, q(5) = 4 * 10^(-5) * 1 = 4 * 10^(-5) Кл.
Теперь нам нужно найти фазу колебаний, которая называется иначе начальной фазой.
Начальная фаза определяется таким значением угла φ, для которого cos(φ) = 1.
В данном случае начальная фаза равна 0, так как cos(0) = 1.
Следовательно, фаза колебаний заряда спустя 5с после начала колебаний равна 0.