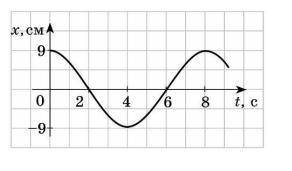
За графіком, наведеним на рисунку, визначте амплітуду та період коливань тіла. Обчисліть частоту та циклічну частоту коливань тіла; запишіть рівняння коливань; знайдіть зміщення тіла у фазі π/3 рад.

Для определения амплитуды и периода колебаний тела на графике необходимо обратить внимание на следующие элементы:

1. Амплитуда колебаний: Амплитуда колебаний определяется как максимальное смещение тела от положения равновесия. На графике это соответствует вертикальной оси исходной точки (A) до самой высокой точки пика и до самой низкой точки долины. Исходя из графика на рисунке, амплитуда колебаний составляет 6.

2. Период колебаний: Период колебаний - это время, за которое тело выполняет одно полное колебание от исходного положения до точки равновесия и обратно. На графике период колебаний может быть определен как расстояние между двумя последовательными пиками или двумя соседними долинами. Исходя из графика на рисунке, период колебаний составляет примерно 3 секунды.

3. Частота колебаний: Частота колебаний - это количество полных колебаний, выполняемых телом за единицу времени. Она обратна периоду колебаний и измеряется в герцах (Гц). Чтобы найти частоту колебаний, необходимо обратиться к формуле:

частота = 1 / период

Исходя из значения периода колебаний, найденного на предыдущем шаге, частота колебаний составляет примерно 1/3 Гц.

4. Циклическая частота колебаний: Циклическая частота колебаний - это угловая скорость, с которой тело выполняет одно полное колебание. Она измеряется в радианах в секунду и может быть вычислена по формуле:

циклическая частота = 2π / период

Исходя из значения периода колебаний, найденного на предыдущем шаге, циклическая частота колебаний составляет примерно 2π/3 рад/с.

5. Равнение колебаний: Равнение колебаний может быть записано в форме:

y = A * sin(ωt + φ)

где:
- y - смещение тела от положения равновесия,
- A - амплитуда колебаний,
- ω - циклическая частота колебаний,
- t - время,
- φ - начальная фаза.

Исходя из значений, найденных на предыдущих шагах, равнение колебаний будет выглядеть следующим образом:

y = 6 * sin((2π/3) t + φ)

6. Змещение тела в фазе π/3 радиан: Змещение тела в определенной фазе может быть найдено подстановкой соответствующих значений в равнение колебаний. В данном случае, чтобы найти змещение тела в фазе π/3 радиан, мы должны приравнять аргумент функции sin в равнении колебаний к π/3:

(2π/3) t + φ = π/3

Затем можно решить это уравнение относительно t, зная начальную фазу φ. Точное решение будет зависеть от значения начальной фазы и может быть найдено с учетом этих данных.