Физика: X=3sin пи/4t найти : скорость, ускорение , кинетическую

X=3sin пи/4t найти : скорость, ускорение , кинетическую

Ответы

wowanuch72 11.10.2020 11:23

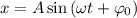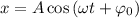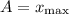Уравнения, которые заданы видом $x = A\sin \left(\omega t + \varphi_{0} \right)$ или $x = A\cos \left(\omega t + \varphi_{0} \right)$ , являются уравнениями гармонических колебаний. Здесь — координата колеблющегося тела (смещение от положения равновесия); $A = x_{\text{max}}$ — амплитуда колебаний; 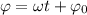$\varphi = \omega t + \varphi_{0}$ — фаза колебаний; 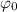$\varphi_{0}$ — начальная фаза колебаний.

Скорость движения тела, совершающего гармонические колебания, — первая производная координаты от времени: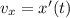 $v_{x}=x'(t)$

Ускорение движения тела, совершающего гармонические колебания, — первая производная скорости от времени, вторая производная координаты от времени: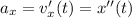 $a_{x} = v_{x}'(t) = x''(t)$

В нашем уравнении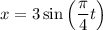 $x = 3\sin \left(\dfrac{\pi}{4}t \right)$ имеем:

$v_{x} = \left(3\sin \left(\dfrac{\pi}{4}t \right) \right)' = \dfrac{3\pi}{4} \cos \left(\dfrac{\pi}{4}t \right)$

$a_{x} = \left(\dfrac{3\pi}{4} \cos \left(\dfrac{\pi}{4}t \right) \right)' = -\dfrac{3\pi^{2}}{16} \sin \left(\dfrac{\pi}{4}t \right)$

Кинетическая энергия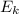 $E_{k}$ — физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы 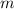тела на квадрат скорости его движения: