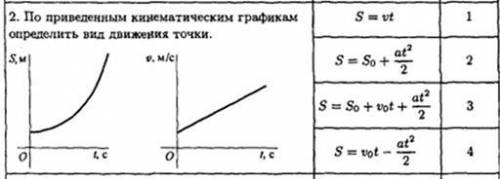
выполнить задание по технической механике! По приведенным кинематическим графикам определить вид движения точки

Значения начальной скорости v₀, конечной скорости v₁, времени движения t₁ снимаем с графика.

Расчётные формулы

а = (v₁, - v₀)/ t₁, - ускорение

s₁ = v₀t₁ + 0.5 at₁² - пройденный путь

v cp = s₁ : t₁ - средняя скорость

График    Вид дв.       v₀, м/с    v₁, м/с    t₁, c    a, м/с²    s₁, м    v ср, м/с    v(t)

    1          равноуск.      2            8          4         1.5         16         4         2 + 1,5t

   2          равнозам.      6            0          3          -2          9          3         6 - 2t

   3          равнозам.      6            2          5        -0,8       20        4         6 - 0,8t            4          равноуск.      0           10          1         10          5         5             10t

Объяснение:

ВОПРОСЫ В КОЕНТЫ! С наступающим новым годом вас!

Добрый день! Конечно, я готов помочь вам разобраться с этим вопросом. Для того чтобы определить вид движения точки по приведенным кинематическим графикам, нам понадобится изучить форму графиков и обратить внимание на особенности каждого из них.

Первый график представляет зависимость скорости от времени. На этом графике скорость показана в зависимости от времени. Если график прямая линия, то скорость постоянна и мы можем сказать, что движение точки равномерное. Если график является прямой линией, обратной или параллельной оси времени, то скорость равна 0 и движение точки неподвижное. Если график представляет собой волнообразные колебания вокруг нулевого значения скорости, то движение точки гармоническое. И, наконец, если график имеет изгибы и не представляет собой равномерно распределенную линию, то скорость изменяется, и движение точки неравномерное.

Второй график показывает зависимость перемещения точки от времени. Если график является прямой линией, то перемещение точки происходит с постоянной скоростью и движение называется равномерным прямолинейным. Если график представлен прямой линией с отрицательным наклоном, то движение происходит с постоянной скоростью, но в обратном направлении. Если график кривой или имеет изгибы, то движение точки неравномерное.

Третий график показывает зависимость ускорения от времени. Если график является прямой линией, то ускорение постоянно и движение точки равноускоренное. Если график является горизонтальной линией, то ускорение равно 0 и движение точки равномерное. Если график представляет собой колебания вокруг нулевого значения ускорения, то движение точки гармоническое. Если график имеет изгибы, то ускорение изменяется, и движение точки неравноускоренное.

Теперь перейдем к решению задачи. На первом графике мы видим, что скорость постоянна и равна 5. Это означает, что движение точки равномерное.

На втором графике наблюдаем, что перемещение точки происходит с постоянной скоростью в положительном направлении, так как график представлен прямой линией со всегда положительным наклоном. Следовательно, движение точки является равномерным прямолинейным.

На третьем графике видим, что ускорение равно 0 на протяжении всего времени. Таким образом, движение точки является равномерным.

Итак, по анализу всех трех графиков можем сделать вывод, что движение точки является равномерным прямолинейным.

Надеюсь, это решение и объяснение помогли вам лучше понять и выполнить задание по технической механике. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задать их!