1. Физика
  2. Вычислить период колебания

Вычислить период колебания маятника и ускорение свободного падения, если за 30 секунд маятник совершил 16 полных колебаний.

1337zezar1 1337zezar1    2   02.10.2019 07:01    3

Ответы
Красавиая123456 Красавиая123456  09.10.2020 11:19
Дано:

Время: t = 30 c.

Количество колебаний: N = 16.

Длина маятника: L.

Найти нужно период и ускорение свободного падения: T, g - ?

Решение:

1. Классическая формула периода колебаний: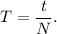 T = \dfrac{t}{N}.

2. Период математического маятника: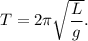 T = 2\pi \sqrt{\dfrac{L}{g}}.

3. Выразим ускорение свободного падения из (2):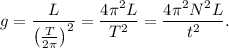 g = \dfrac{L}{\left(\frac{T}{2\pi}\right)^2} = \dfrac{4\pi ^2L}{T^2} = \dfrac{4\pi ^2N^2L}{t^2}.

Численно получим:

T = \dfrac{30}{16} = 1,875 (c).

g = \dfrac{4*3,14^2*16^2L}{30^2} = 0,7L (м/с²).

L подставите и досчитаете :)

ответ: 1,875 с; 0,7L м/с².
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Rebefullik4 Rebefullik4  08.08.2019 08:00
Встальной кастрюле массой 1,2 кг налито 2 литра воды с температурой 20 ° c. необходимо нагреть воду до 25 ° c.сколько нужно сжечь природного газа, если вся теплота выделившаяся...
1234567891243 1234567891243  08.08.2019 08:00
Определите предел измерений мензурки,цену деления и объем жижкости налитой в мензурку. там вот такой рисунок шкалы мензурки: _ _ _ _ (до этой линии налита жидкость) _ _...
kkkkiiiii kkkkiiiii  08.08.2019 08:00
Скажите , что это за формулы ( что они обозначают ), буду q=cm(t2-t1) c= q/c(t2-t1) (t2-t1)=q/cm...
sponsor1776 sponsor1776  08.08.2019 08:00
По уравнению координаты х=6+2t+6t^2 определите: начальную скорость, проекцию ускорения, начальную координату...
khairulliniljap00rzn khairulliniljap00rzn  08.08.2019 08:00
Автомобіль 3 км рухався зі швидкістю 40 км за год і потім ще 3 км - зі швидкістю 60 км за год. яка середня швидкість руху автомобіля на цьому шляху?...
Muzahabiba Muzahabiba  08.08.2019 08:00
Какого длина траектории движения секундной стрелки...
123киівміша 123киівміша  15.08.2019 08:00
Банка объёмом 2 дм3 заполнена подсолнечным маслом . вычисли вес подсолнечного масла....
dinnaasv dinnaasv  15.08.2019 08:00
Резонирующий бокал бокал, частично заполненный жидкостью, будет резонировать при воздействии звука из громкоговорителя. исследуйте, как явление зависит от различных параметров....
Елдиор Елдиор  02.06.2019 23:50
Определите сопротивление никелиновой проволоки длиной 4 м и площядью поперечного сечения 2 мм (в квадрате). какова сила тока в этой проволоке при напряжения на ее концах...
vanya33251243 vanya33251243  16.05.2021 19:37
Имя тоже kik dinko приз напишите...

Популярные вопросы