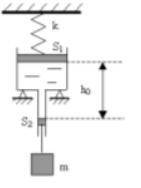
В вертикально расположенном сосуде с сечениями S1 и S2 (S1 = 9S2) находятся два невесомых поршня. Пространство между
поршнями заполнено водой. Концы сосуда открыты в
атмосферу. К верхнему поршню прикреплена пружина
жесткостью k, к нижнему подвешен груз массой m. В начальный
момент времени пружина не растянута, поршни закреплены,
расстояние между поршнями h0. Найдите, на сколько просядет
верхний поршень, если оба поршня отпустить

Для решения данной задачи, нам необходимо использовать законы Архимеда, закон Гука и второй закон Ньютона.

1. Закон Архимеда гласит, что на тело, погруженное в жидкость или газ, действует сила, равная весу вытесненной жидкости или газа. В нашем случае, вода вытесняется поршнями и на каждый поршень действует сила Архимеда.

2. Закон Гука гласит, что деформация пружины пропорциональна действующей на нее силе. В нашем случае, пружина сжимается под действием груза и создает противодействующую силу натяжения.

3. Второй закон Ньютона гласит, что сумма всех сил, действующих на тело, равна произведению массы тела на его ускорение. В нашем случае, ускорение верхнего поршня будет противоположно направлено его движению, так как верхний поршень просядет вниз.

Теперь перейдем к решению задачи пошагово:

Шаг 1: Найдем силу Архимеда, действующую на верхний поршень.
Сила Архимеда определяется по формуле:
Fa = ρ * g * V,
где Fa - сила Архимеда,
ρ - плотность жидкости,
g - ускорение свободного падения,
V - объем вытесненной жидкости.

Объем вытесненной жидкости можно найти по формуле:
V = S1 * h,
где S1 - площадь сечения верхнего поршня,
h - проседание верхнего поршня.

Таким образом, мы можем записать:
Fa = ρ * g * (S1 * h).

Шаг 2: Найдем силу натяжения пружины.
Сила натяжения пружины определяется по закону Гука:
Fh = k * Δl,
где Fh - сила натяжения пружины,
k - жесткость пружины,
Δl - деформация пружины.

Деформация пружины равна разности длинны пружины до и после сжатия:
Δl = l - l0,
где l0 - исходная длина пружины,
l - длина пружины после сжатия.

Мы можем записать:
Fh = k * (l - l0).

Шаг 3: Найдем силу, с которой груз давит на нижний поршень.
Сила, с которой груз давит на нижний поршень, равна его весу:
Fm = m * g,
где Fm - сила, с которой груз давит на нижний поршень,
m - масса груза.

Шаг 4: Запишем второй закон Ньютона для верхнего поршня.
Сумма всех сил, действующих на верхний поршень, должна быть равна произведению его массы на его ускорение:
Fa - Fh - Fm = m * a,
где a - ускорение верхнего поршня.

Мы можем записать:
ρ * g * (S1 * h) - k * (l - l0) - m * g = m * a.

Шаг 5: Найдем проседание верхнего поршня.
Для этого из уравнения второго закона Ньютона выразим h:
h = (m * a + k * (l - l0) - m * g) / (ρ * g * S1).

Шаг 6: Подставим известные значения и решим уравнение.
В задаче даны следующие значения:
S1 = 9S2,
l0 = 0,
S1 = 9S2,
m = 2кг,
k = 10 N/м,
ρ = 1000 кг/м^3,
g = 9,8 м/с^2.

Подставим эти значения в уравнение:
h = (2кг * a + 10N/м * (l - 0) - 2кг * 9,8м/с^2) / (1000кг/м^3 * 9,8м/с^2 * 9S2).

Шаг 7: Преобразуем уравнение.
h = (2a + 10(l - 0) - 19,6) / (88200S2).

Учитывая, что S1 = 9S2, мы можем записать:
h = (2a + 10(l - 0) - 19,6) / (88200 * S1 / 9).

Шаг 8: Упростим уравнение и найдем окончательное выражение для проседания верхнего поршня.
h = (18a + 90l - 176,4) / (8820S1).

Таким образом, проседание верхнего поршня будет равно (18a + 90l - 176,4) / (8820S1).