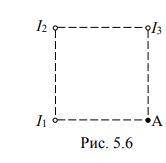
В трёх вершинах квадрата со стороной а перпендикулярно его плоскости расположены длинные прямые проводники, по которым текут токи I1, I2,
I3 одного направления, I2 = 20 А, I1 = I3При этом индукция магнитного поля в точке А, дающей с четвертой вершиной квадрата, В = 11,310-5 Тл. Если изменить
направление тока I2 на противоположное, индукция поля в точке А изменится в 2 раза. Определить длину стороны квадрата и силу токов I1 и I
Другие вопросы по теме Физика
Популярные вопросы
- Было семь гнезд. в каждом гнезде по 3 яйца. сколько вылупилось птенцов,...
1 - Угол наклона оси вращения земли к плоскости орбиты равен: 1)25,5° 2)36,5°...
2 - 1.сколько 3-х значных чисел можно составить из цифр 0,2,4,6 с условием,что...
2 - Усаши в игрушечном аквариуме рыбки на магнитах: 3 красных, 13 синих,4...
3 - Сочинение на тему семья, школа и родина в моей жизни...
3 - Определи сколько времени длится двухсерийный через телесериал если продолжительность...
2 - Вкиоске воздушные шарики четырёх цветов. сколько существует вариантов...
3 - Сколько часов в: 1) 11 минутах 2) 35 минутах 3) 75 минутах 4) 1 часу...
3 - Желательно быстро. известно, что 15...
1 - Переведите правильно , в переводчике ничего не получается , заранее !...
3
Первое, что требуется найти в этой задаче, - это длина стороны квадрата (a) и силы токов I1 и I3.
Для начала, вспомним формулу для расчета магнитной индукции вблизи прямого провода:
B = (μ0 * I) / (2 * π * r)
где:
B - магнитная индукция,
μ0 - магнитная постоянная, равная примерно 4π * 10^(-7) Тл * м/А,
I - ток в проводнике,
r - расстояние от точки до проводника.
Из условия задачи мы знаем, что индукция магнитного поля в точке А равна B = 11,3 * 10^(-5) Тл. Согласно задаче, это значение будет изменяться в 2 раза при изменении направления тока I2.
Заметим, что при изменении направления тока, индукция магнитного поля в точке А изменяется в 2 раза. Это означает, что в исходной ситуации, когда ток I2 имеет изначальное направление, индукция магнитного поля в точке А равна половине значения после изменения направления тока I2. То есть, в исходной ситуации B = 11,3 * 10^(-5) Тл / 2.
Найдем теперь силу тока I2. Мы знаем, что сила тока I2 равна 20 А в исходной ситуации. Также, из условия задачи следует, что направление тока I2 меняется на противоположное. То есть, после изменения направления тока I2, сила тока I2 будет составлять -20 А.
Рассмотрим теперь положительное направление тока I2. По правилу "Био-Савара-Лапласа" сумма векторов магнитных полей, создаваемых токами I1, I2 и I3, должна быть равна магнитному полю, измеряемому в точке А. Это означает, что
B = B1 + B2 + B3.
Распишем это равенство:
B = (μ0 * I1) / (2 * π * r1) + (μ0 * I2) / (2 * π * r2) + (μ0 * I3) / (2 * π * r3),
где r1, r2, r3 - расстояния от точки А до проводников с токами I1, I2 и I3 соответственно.
Используя полученные данные из условия задачи, мы можем записать:
B = (μ0 * I1) / (2 * π * a) + (μ0 * 20) / (2 * π * a) + (μ0 * I3) / (2 * π * a).
Мы знаем, что в исходной ситуации, до изменения направления тока I2, индукция магнитного поля B равнялась половине значения после изменения направления тока I2:
11,3 * 10^(-5) Тл / 2 = (μ0 * I1) / (2 * π * a) + (μ0 * 20) / (2 * π * a) + (μ0 * I3) / (2 * π * a).
Теперь мы можем выразить силу тока I1 через силу тока I3:
(μ0 * I1) / (2 * π * a) = (11,3 * 10^(-5) Тл / 2) - (μ0 * 20) / (2 * π * a) - (μ0 * I3) / (2 * π * a).
Также из условия задачи мы знаем, что сила тока I1 равняется силе тока I3:
I1 = I3.
Подставим это равенство в последнее уравнение:
(μ0 * I1) / (2 * π * a) = (11,3 * 10^(-5) Тл / 2) - (μ0 * 20) / (2 * π * a) - (μ0 * I1) / (2 * π * a).
Решим это уравнение:
2 * (μ0 * I1) / (2 * π * a) = 11,3 * 10^(-5) Тл / 2 - 20 * μ0 / (2 * π * a).
2 * (μ0 * I1) = (11,3 * 10^(-5) Тл / 2 - 20 * μ0) * a / π.
2 * (4π * 10^(-7) Тл * I1) = (11,3 * 10^(-5) Тл / 2 - 20 * 4π * 10^(-7) Тл) * a / π.
8π * 10^(-7) Тл * I1 = (11,3 * 10^(-5) Тл / 2 - 80π * 10^(-7) Тл) * a / π.
8π * 10^(-7) Тл * I1 = 11,3 * 10^(-5) Тл / 2 - 80π * 10^(-7) Тл / π * a.
8π * 10^(-7) Тл * I1 = 11,3 * 10^(-5) Тл / 2 - 80 * 10^(-7) Тл * a.
Теперь мы можем найти значение силы тока I1:
I1 = (11,3 * 10^(-5) Тл / 2 - 80 * 10^(-7) Тл * a) / (8π * 10^(-7) Тл).
А также, используя равенство I1 = I3, найдем значение силы тока I3:
I3 = (11,3 * 10^(-5) Тл / 2 - 80 * 10^(-7) Тл * a) / (8π * 10^(-7) Тл).
Таким образом, получаем формулу для нахождения сил токов I1 и I3 через длину стороны квадрата (a) и индукцию магнитного поля в точке А. Остается только подставить значения в эту формулу и решить уравнение, чтобы найти значения сил токов.