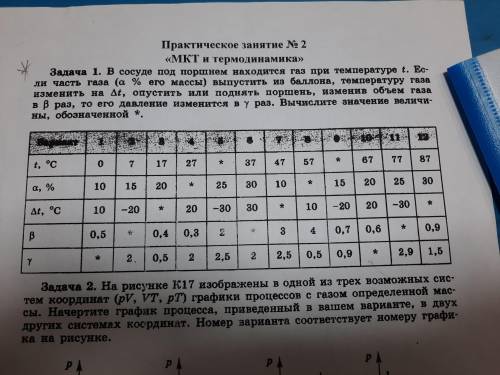
В сосуде под поршнем находится газ при температуре 47. Если часть газа 10 выпустить из , температуру газа изменить на (дельта) t x, опустить или поднять поршень, изменив, объем газа в B раз, то его давление изменится в 2,5 раз. ВЫЧИСЛИТЕ ЗНАЧЕНИЕ ДЕЛЬТА t

Для решения этой задачи нам понадобятся такие основные понятия как закон Гей-Люссака и закон Бойля-Мариотта.

Закон Гей-Люссака связывает изменение температуры газа с его объемом при постоянном давлении и количестве вещества. Формула закона Гей-Люссака выглядит следующим образом:
V₁ / T₁ = V₂ / T₂,
где V₁ и V₂ - исходный и измененный объемы газа,
T₁ и T₂ - исходная и измененная температуры газа.

Закон Бойля-Мариотта связывает изменение объема газа с его давлением при постоянной температуре и количестве вещества. Формула закона Бойля-Мариотта выглядит следующим образом:
P₁ * V₁ = P₂ * V₂,
где P₁ и P₂ - исходное и измененное давление газа,
V₁ и V₂ - исходный и измененный объемы газа.

В нашей задаче у нас есть следующие данные:
Температура газа до изменений - T₁ = 47.
Объем газа изменяется в B раз.
Давление газа изменяется в 2,5 раз.

Поскольку изменение давления связано с объемом газа, мы можем использовать закон Бойля-Мариотта, чтобы выразить изменение объема через изменение давления:
P₁ * V₁ = P₂ * V₂.
Поскольку P₁ и V₁ неизвестны, мы можем использовать их как переменные (назовем их x и y соответственно):
x * V₁ = 2,5 * y.

Также у нас есть изменение температуры, которое обозначено как Δt. Используя закон Гей-Люссака, мы можем записать соотношение между исходными и измененными значениями температуры:
V₁ / T₁ = V₂ / (T₁ + Δt).

Теперь у нас есть два уравнения:
x * V₁ = 2,5 * y,
V₁ / T₁ = V₂ / (T₁ + Δt).

Мы можем решить эти два уравнения для нахождения Δt. Для этого поэтапно решим систему уравнений:

1. Решим первое уравнение для V₁:
x * V₁ = 2,5 * y,
V₁ = (2,5 * y) / x.

2. Подставим это значение V₁ во второе уравнение:
((2,5 * y) / x) / T₁ = V₂ / (T₁ + Δt).

3. Упростим уравнение, умножив обе части на x * T₁:
2,5 * y * T₁ = x * V₂ * (T₁ + Δt).

4. Разрешим уравнение относительно Δt:
2,5 * y * T₁ = x * V₂ * T₁ + x * V₂ * Δt,
2,5 * y * T₁ - x * V₂ * T₁ = x * V₂ * Δt,
Δt = (2,5 * y * T₁ - x * V₂ * T₁) / (x * V₂).

Итак, мы получили формулу для вычисления Δt:
Δt = (2,5 * y * T₁ - x * V₂ * T₁) / (x * V₂).

Теперь мы можем заменить значения y, T₁, x и V₂ и вычислить Δt.