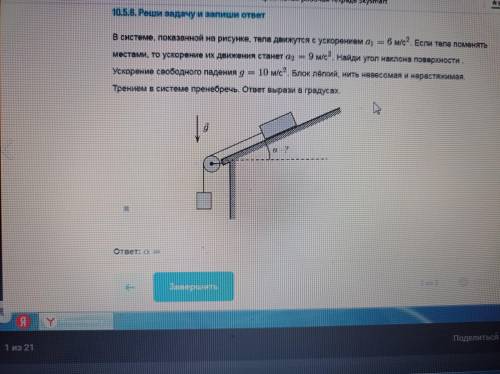
В системе,показанной на рисунке,тела движутся с ускорением a1=6 м/с^2. Если тела поменять местами,то ускорение их движения станет a2=9 м/с^2. Найди угол наклона поверхности. Ускорение свободного падения g=10 м/с^2. Блок лëгкий,нить невесомая и нерастяжимая. Трением силы пренебречь. ответ вырази в градусах. С подробным решением.
Другие вопросы по теме Физика
Популярные вопросы
- Суровнением 5х- 7 0.2х +3.2 = 3 0.3...
2 - Подобные слагаемые: 0,6x+3,5y-2,7y...
1 - Из двух сём, расстояние между которыми 82,4 км, одновременно навстречу друг...
2 - Решите уравнения а) 8,4-(х-7,2)=8,6 б) -1,3+(х-4,8)=-7,1...
1 - Укажите названия городов. являющихся столицами княжеств в xii веке. 1.владимир...
3 - Решите примеры: (-1)-3+8(++6) и...
1 - Почему,говоря о средствах языка,прежде всего называют слово? каково его первейшее...
2 - Корове заготовили на день 40 кг корма. четвертую часть этого корма составляло...
1 - Рассказ о традициях татар из века в век....
3 - Моторная лодка проплыла 200 метров за 30 секунд какова скорость лодки 20 километров...
2
Из условия задачи мы знаем, что ускорение тела 1 равно a1 = 6 м/с^2, а ускорение тела 2 равно a2 = 9 м/с^2. Заметим, что ускорения направлены в разные стороны, в зависимости от положения тел.
Обозначим массу тела 1 как m1 и массу тела 2 как m2.
Рассмотрим силы, действующие на тела:
- На тело 1 действует сила тяжести F1 = m1 * g (где g - ускорение свободного падения).
- На тело 1 также действует сила натяжения нити, направленная вдоль поверхности и равная T.
- На тело 2 действует сила тяжести F2 = m2 * g.
- На тело 2 также действует сила натяжения нити, направленная вверх и равная T.
Теперь мы можем применить второй закон Ньютона для каждого из тел:
- Для тела 1: m1 * a1 = m1 * g - T.
- Для тела 2: m2 * a2 = T - m2 * g.
Так как у нас заданы значения ускорений a1 и a2, а также ускорение свободного падения g, мы можем записать систему уравнений:
m1 * 6 = m1 * 10 - T.
m2 * 9 = T - m2 * 10.
Выразим T из первого уравнения и подставим во второе уравнение:
T = m1 * 10 - 6m1.
m2 * 9 = (m1 * 10 - 6m1) - m2 * 10.
Раскроем скобки и упростим выражение:
9m2 = 10m1 - 6m1 - 10m2.
9m2 + 10m2 = 10m1 - 6m1.
19m2 = 4m1.
Делим обе части уравнения на 4m1:
19m2 / (4m1) = 1.
19m2 = 4m1.
m2/m1 = 4/19.
Теперь мы можем выразить T:
T = m1 * 10 - 6m1.
T = m1 * (10 - 6).
T = 4m1.
Подставим найденное значение T в первое уравнение:
m1 * 6 = m1 * 10 - 4m1.
6m1 = 10m1 - 4m1.
6m1 + 4m1 = 10m1.
10m1 = 10m1.
Таким образом, мы видим, что массы тела не влияют на значения ускорений и сил натяжения нити. Это значит, что верхний и нижний блоки имеют равные массы.
Далее, чтобы найти угол наклона поверхности, нам понадобится знать отношение ускорений и сил тяжести тел.
Ускорение тела 1 по направлению вдоль поверхности равно a1 = 6 м/с^2, а ускорение тела 2 по направлению вверх равно a2 = 9 м/с^2.
На тело 1 действует сила тяжести F1 = m1 * g, направленная вниз, и сила натяжения нити T, направленная вверх.
На тело 2 действует сила тяжести F2 = m2 * g, направленная вниз, и сила натяжения нити T, направленная вверх.
По второму закону Ньютона для тела 1: m1 * a1 = m1 * g - T.
По второму закону Ньютона для тела 2: m2 * a2 = T - m2 * g.
Мы можем выразить T из первого уравнения: T = m1 * g - m1 * a1.
Теперь мы можем подставить выражение для T во второе уравнение и решить его:
m2 * a2 = (m1 * g - m1 * a1) - m2 * g.
Раскрываем скобки и упрощаем выражение:
m2 * a2 = m1 * g - m1 * a1 - m2 * g.
Теперь сгруппируем члены с m1 и m2:
m2 * a2 + m2 * g = m1 * g - m1 * a1.
Выразим m2 из этого уравнения:
m2 = (m1 * g - m1 * a1) / (a2 + g).
Так как мы знаем отношение масс m2/m1 = 4/19, подставим это значение в уравнение:
4/19 = ((m1 * g - m1 * a1) / (a2 + g)) / m1.
Упростим выражение:
4/19 = (g - a1) / (a2 + g).
Выразим угол наклона поверхности и преобразуем уравнение:
4(a2 + g) = 19(g - a1).
Раскроем скобки и упростим уравнение:
4a2 + 4g = 19g - 19a1.
Перенесем все слагаемые с a2 на одну сторону уравнения:
4a2 + 19a1 = 19g - 4g.
4a2 + 19a1 = 15g.
Теперь мы можем выразить угол наклона поверхности:
Так как a = g * sin(θ), где θ - угол наклона поверхности, то
4a2 + 19a1 = 15g * sin(θ).
Для нашей задачи g = 10 м/с^2, a1 = 6 м/с^2 и a2 = 9 м/с^2:
4 * (9)^2 + 19 * 6 = 15 * 10 * sin(θ).
Вычислим выражение в левой части уравнения:
4 * 81 + 19 * 6 = 150 * sin(θ).
324 + 114 = 150 * sin(θ).
438 = 150 * sin(θ).
Теперь найдем sin(θ):
sin(θ) = 438 / 150.
sin(θ) ≈ 2.92.
Так как мы ищем угол, выразим θ через арксинус:
θ ≈ arcsin(2.92).
Используя калькулятор, находим значение арксинуса(2.92):
θ ≈ 1.29 радиан.
Для ответа в градусах, переведем радианы в градусы:
θ (в градусах) ≈ 1.29 * (180 / π).
θ (в градусах) ≈ 73.86°.
Таким образом, угол наклона поверхности составляет около 73.86 градусов.