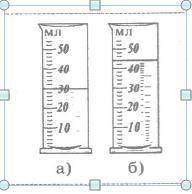
В мензурку налит глицерин (рис.а). Его плотность 1260 кг/м3 . Потом глицерина добавили еще (рис.б). Определите массу долитого в мензурку глицерина.

Чтобы определить массу долитого глицерина в мензурку, мы должны использовать следующую формулу:

масса = объем × плотность

На рисунке а мы видим, что в мензурке налит определенный объем глицерина. Давайте назовем его V_1. Значение V_1 мы не знаем, поэтому возьмем его равным неизвестной переменной x.

Таким образом, масса глицерина на рисунке а будет равна:
масса_а = V_1 × плотность глицерина

Затем на рисунке б глицерин был долит до определенного объема (объем V_2), который также является неизвестным. Поэтому мы также предположим, что объем долитого глицерина равен переменной y.

Мы знаем, что плотность глицерина остается той же самой, поэтому масса_б нового глицерина, который был долит в мензурку, будет равна:
масса_б = y × плотность глицерина

Нам нужно определить массу долитого глицерина, поэтому мы складываем массу_а и массу_б:
масса_долитого_глицерина = масса_а + масса_б

Теперь мы можем составить уравнение, используя формулу массы:
масса_долитого_глицерина = (V_1 × плотность глицерина) + (y × плотность глицерина)

По условию задачи нам дана плотность глицерина: 1260 кг/м3. Давайте заменим ее в нашем уравнении:
масса_долитого_глицерина = (V_1 × 1260) + (y × 1260)

Теперь нам нужно связать объемы V_1 и V_2 в нашем уравнении.

На рисунке а, глицерин заполняет только часть мензурки, а на рисунке б он заполняет уже всю. То есть, объем долитого глицерина равен объему мензурки (обозначим его V_мензурки) после доливки.

Это означает, что:
V_2 = V_мензурки

Нам нужно найти массу долитого глицерина, поэтому мы заменим V_2 в нашем уравнении:
масса_долитого_глицерина = (V_1 × 1260) + (V_2 × 1260)

Мы также знаем, что V_2 (объем мензурки после доливки) равен сумме объема глицерина на рисунке а и объема глицерина на рисунке б:
V_2 = V_1 + y

Теперь мы можем заменить V_2 в нашем уравнении:
масса_долитого_глицерина = (V_1 × 1260) + ((V_1 + y) × 1260)

У нас все еще есть две неизвестные: V_1 и y. Нам нужно еще одно уравнение, чтобы решить эту систему уравнений.

Обратите внимание, что глицерин является несжимаемой жидкостью, поэтому объем глицерина в системе остается неизменным в ходе доливки. Это означает, что общий объем глицерина в системе равен сумме объема глицерина на рисунке а и объема глицерина на рисунке б:

V_глицерина_в_системе = V_1 + (V_2 - V_1)

У нас есть равенство объемов V_глицерина_в_системе и V_мензурки. Мы можем заменить V_глицерина_в_системе и V_мензурки нашими переменными:
V_1 + (V_1 + y) = V_мензурки

Решим это уравнение для y:
2V_1 + y = V_мензурки
y = V_мензурки - 2V_1

Теперь, используя найденное значение y, мы можем заменить его в нашем уравнении для массы_долитого_глицерина:
масса_долитого_глицерина = (V_1 × 1260) + ((V_1 + (V_мензурки - 2V_1)) × 1260)

Дальше вам нужно знать значения V_1 и V_мензурки, чтобы получить окончательный ответ.