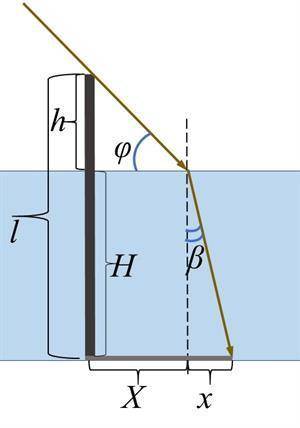
В дно водоёма вбита свая длиной l= 1,64 м. Свая возвышается над поверхностью воды на h= 0,82 м. Угол между горизонтом и лучами солнца, падающими на поверхность воды, равен ϕ = 30°. Определи длину тени от сваи на дне водоёма, если показатель преломления воды равен n= √3. 1. Глубина водоёма равна H= __м. (Округли до сотых).
2. Угол падения светового луча на поверхность воды равен α =__°.
3. Угол преломления равен β =__°.
4. Длина тени равна L=X+x=__м. (Округли до сотых).
Grechk
3
15.05.2021 23:12
0
Другие вопросы по теме Физика
topovyjpocan
26.11.2020 12:16
Hictoru
26.11.2020 12:16
аноним12345567808
26.11.2020 12:16
1ivel3
26.11.2020 12:16
nikoldasha421
26.11.2020 12:16
9ky3ya
26.11.2020 12:16
gandzofficial
26.11.2020 12:16
maksim5a
26.11.2020 12:17
2003kate2003kate2003
26.11.2020 12:17
Популярные вопросы
- 2. Суретте көлбеу жазықтық берілген.Көлбеу жазықтықтың бетінде массасы...
3 - Напишите о человеке, чьё творчество сейчас вас радует...
3 - итоговая контрольная работа по немецкому. очень нужно....
2 - 1.Кермектілікті туындататын катиондар Mg 2+ және Ca 2+...
1 - Света, Даша и Оля разделили между собой 120 жевательных конфет. Света...
1 - Від поданих числівники записати порядкового числівники 2 сотні , 15...
3 - Русский язык 6 класс страница 189 по вариантам ...
2 - Установите правильное соответствие между датой и событием Даты:  1581...
1 - 1. Последовательность действий, выполнение которых приводит к конечному...
1 - Поміркуйте, зі скількох частин складаються подані безсполучникові складні...
2
Объяснение:
Дано:
l = 1,64 м
h = 0,82 м
φ = 30°
n = √3
1. Глубина водоёма:
H = l - h = 1,64 - 0,82 = 0,82 м.
2. Угол падения светового луча на поверхность воды равен:
α = 90° - φ = 90° - 30° = 60°.
3. Угол преломления равен:
n = sin α / sin β
sin β = sin α / n = √3 / (2·√3) = 1/2
β = 30°
4. Длина тени равна:
L = X + x = h/tg φ + H·tgβ
L = 0,82/tg 30° + 0,82·tg30° = 0,82 ( 3/√3 + √3/3) ≈ 1,89 м