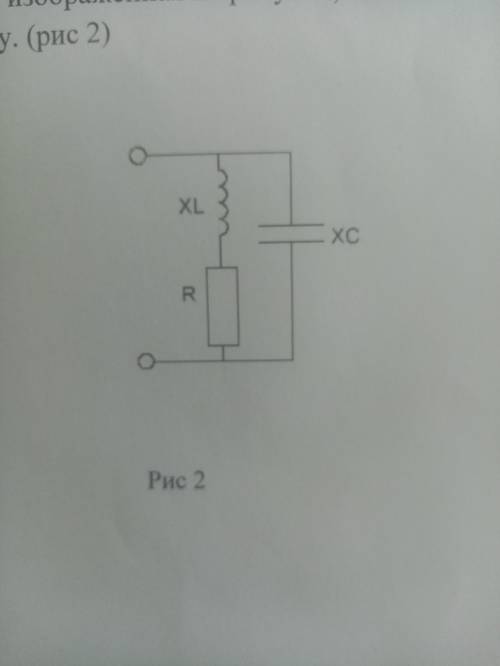
УМОЛЯЮ какой характер нагрузки будет носить цепь, изображенная на рисунке, если XC=XL=R. Построить векторную диаграмму

Дорогой школьник,

На данном рисунке, изображена электрическая цепь, состоящая из источника переменного тока (изображенного как "V") и элементов нагрузки - соединенных последовательно резистора (R), катушки индуктивности (XL) и конденсатора (XC).

Тебя интересует, какой характер нагрузки будет носить эта цепь, если сопротивление конденсатора (XC) равно сопротивлению катушки индуктивности (XL) и резистора (R).

Для начала, давай определим, что такое "характер нагрузки". Характер нагрузки определяется отношением между током и напряжением в цепи. В данном случае, мы будем строить векторную диаграмму, чтобы наглядно представить это отношение.

Теперь, чтобы построить векторную диаграмму, нам нужно знать амплитудное значение напряжения и фазы тока. Для упрощения, будем считать, что источник переменного тока имеет амплитудное значение напряжения "V" и ток "I" с нулевой фазой.

Так как сопротивления конденсатора (XC), катушки индуктивности (XL) и резистора (R) одинаковы, то их реактивные сопротивления также будут равны друг другу. Реактивное сопротивление катушки индуктивности выражается через индуктивность (L) и угловую частоту (ω) как XL = ωL, а реактивное сопротивление конденсатора выражается через ёмкость (C) и угловую частоту (ω) как XC = 1/(ωC). Из условия задачи, мы знаем, что XL = XC = R.

Поскольку XL = XC, то мы можем записать: ωL = 1/(ωC). Раскроем это уравнение. Перенесем ω на одну сторону и C на другую сторону уравнения:
ω^2 = 1/(LC)

Заметим, что в правой части уравнения находится величина, обратная произведению индуктивности и ёмкости (LC). Из этого мы можем сделать вывод, что если индуктивность и ёмкость в цепи таковы, что их произведение равно единице, то ω^2 также будет равно единице. Это означает, что ω = 1.

Учитывая это значение угловой частоты, мы можем выразить реактивное сопротивление (XL) через индуктивность (L): XL = ωL = 1L = L.

Таким образом, у нас получилось, что реактивное сопротивление катушки индуктивности (XL) равно сопротивлению катушки.

Теперь, для построения векторной диаграммы, нам нужно учесть фазы тока в каждом элементе цепи. В данном случае, так как элементы цепи соединены последовательно, то фаза тока будет одинакова во всей цепи.

Давай обозначим фазу тока как φ. Тогда, фаза тока в резисторе (R), катушке индуктивности (XL) и конденсаторе (XC) будет равна φ.

Теперь мы готовы построить векторную диаграмму. На диаграмме, мы будем использовать горизонтальную ось для изображения напряжения, а вертикальную ось для изображения тока.

Рисунок (1) :
На векторной диаграмме, мы рисуем вектор напряжения V вдоль горизонтальной оси. Затем, из начала этого вектора проводим вектор тока I под углом φ вверх.

Рисунок (2) :
Затем, мы рисуем вектор напряжения на резисторе (R), равный RI, под углом 0 вдоль горизонтальной оси.

Рисунок (3) :
После этого, мы рисуем вектор напряжения на катушке индуктивности (XL), равный XLI, под углом φ вверх.

Рисунок (4) :
И, наконец, мы рисуем вектор напряжения на конденсаторе (XC), равный XCI, под углом φ вниз.

Теперь, чтобы ответить на вопрос о характере нагрузки, мы должны анализировать геометрическую конфигурацию векторной диаграммы.

Здесь, векторы напряжения на резисторе (R) и катушке индуктивности (XL) имеют одинаковую ориентацию (вертикально вверх), но вектор напряжения на конденсаторе (XC) имеет противоположную ориентацию (вертикально вниз).

Это означает, что мы имеем два вектора суммирующиеся по вертикальной оси, но вектор на конденсаторе (XC) компенсирует некоторую часть вектора на катушке индуктивности (XL). Точнее говоря, вектор на конденсаторе (XC) компенсирует реактивное сопротивление катушки индуктивности (XL).

Следовательно, нагрузка на цепь будет носить резистивный характер, так как реактивности компенсируют друг друга.

Я надеюсь, что данное объяснение позволяет тебе лучше понять, какой характер нагрузки будет носить эта цепь и что именно происходит внутри нее. Если у тебя возникнут еще вопросы, не стесняйся задать их. Я всегда готов помочь.

Удачи в учебе!